अध्याय 10 : गुरुत्वाकर्षण (Gravitation)
हमारे चारों ओर की हर वस्तु पृथ्वी की ओर खिंचती है — चाहे वह पेड़ से गिरता हुआ फल हो या हम स्वयं।
इस आकर्षण बल को गुरुत्वाकर्षण बल (Gravitational Force) कहा जाता है।
यह प्रकृति का एक मूलभूत बल है जो सभी वस्तुओं को उनके द्रव्यमान के कारण एक-दूसरे की ओर आकर्षित करता है।
गुरुत्वाकर्षण का सिद्धांत सर्वप्रथम सर आइज़ैक न्यूटन (Sir Isaac Newton) ने प्रतिपादित किया था जब उन्होंने पेड़ से गिरते हुए एक सेब को देखा था।
गुरुत्वाकर्षण बल की परिभाषा
दो वस्तुओं के बीच उनके द्रव्यमान के कारण लगने वाला आकर्षण बल गुरुत्वाकर्षण बल कहलाता है।
यह बल प्रत्येक वस्तु को दूसरी वस्तु की ओर खींचता है।
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण का नियम
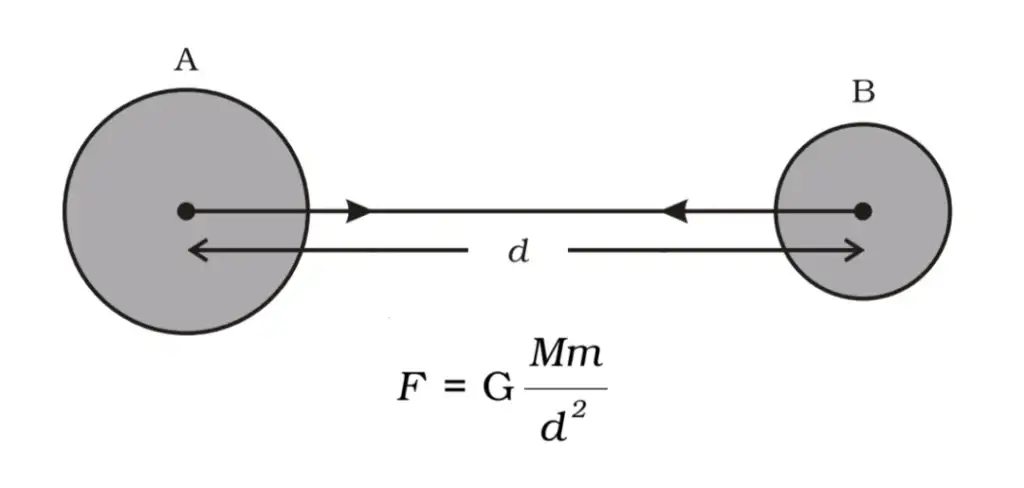
न्यूटन के अनुसार — “संसार की प्रत्येक वस्तु दूसरी वस्तु को एक बल से आकर्षित करती है जो उनके द्रव्यमानों के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।”
जहाँ,
F = गुरुत्वाकर्षण बल
G = सार्वत्रिक गुरुत्वाकर्षण नियतांक (6.67 × 10⁻¹¹ N·m²/kg²)
m₁, m₂ = वस्तुओं के द्रव्यमान
r = उनके बीच की दूरी
गुरुत्व त्वरण (Acceleration due to Gravity)
जब कोई वस्तु पृथ्वी के गुरुत्वाकर्षण के कारण गिरती है, तो वह एक नियत त्वरण से गिरती है, जिसे गुरुत्व त्वरण (g) कहा जाता है।
पृथ्वी की सतह पर इसका मान लगभग 9.8 m/s² होता है।
| स्थान | गुरुत्व त्वरण (m/s²) |
|---|---|
| भूमध्य रेखा पर | 9.78 |
| ध्रुवों पर | 9.83 |
गुरुत्वाकर्षण के प्रयोग और महत्व
- यह पृथ्वी के वातावरण को बनाए रखता है।
- यह ग्रहों को सूर्य के चारों ओर परिक्रमा करने में मदद करता है।
- वर्षा, ज्वार-भाटा और वस्तुओं के गिरने जैसी घटनाएँ इसी के कारण होती हैं।
गुरुत्वाकर्षण का सार्वत्रिक नियम (Universal Law of Gravitation)
हम जानते हैं कि पृथ्वी हमें अपनी ओर खींचती है। लेकिन क्या केवल पृथ्वी ही वस्तुओं को आकर्षित करती है?
नहीं — वास्तव में, ब्रह्माण्ड की प्रत्येक वस्तु दूसरी वस्तु को एक बल से अपनी ओर आकर्षित करती है।
इस बल को ही गुरुत्वाकर्षण बल (Gravitational Force) कहते हैं, और इस पर आधारित नियम को
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण का नियम कहा जाता है।
सर आइज़ैक न्यूटन ने कहा —
“संसार की प्रत्येक वस्तु दूसरी वस्तु को एक बल से आकर्षित करती है,
जो उनके द्रव्यमानों के गुणनफल के समानुपाती और उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।”
गणितीय रूप में:
जहाँ,
F = दो वस्तुओं के बीच लगने वाला गुरुत्वाकर्षण बल
m₁ = पहली वस्तु का द्रव्यमान
m₂ = दूसरी वस्तु का द्रव्यमान
r = दोनों वस्तुओं के बीच की दूरी
G = सार्वत्रिक गुरुत्वाकर्षण नियतांक (Universal Gravitational Constant)
यह एक नियतांक है और पूरे ब्रह्माण्ड में समान रहता है।
समानुपात से सूत्र की व्युत्पत्ति (Derivation by Proportionality)
न्यूटन के अनुसार:
- बल वस्तुओं के द्रव्यमान के गुणनफल के समानुपाती है:
F ∝ (m₁ × m₂) - बल दूरी के वर्ग के व्युत्क्रमानुपाती है:
F ∝ 1/r²
इन दोनों को मिलाकर:
F ∝ (m₁ × m₂) / r²
या,
F = G × (m₁ × m₂) / r²
बल की दिशा
यह बल सदैव उन दोनों वस्तुओं के केंद्रों को जोड़ने वाली रेखा की दिशा में लगता है।
दोनों वस्तुएँ एक-दूसरे को समान परिमाण के बल से विपरीत दिशा में खींचती हैं।
यह न्यूटन के तृतीय नियम (Action-Reaction Law) के अनुरूप है।
उदाहरण:
यदि दो पिंडों का द्रव्यमान क्रमशः 10 kg और 20 kg है और उनके बीच की दूरी 2 m है, तो उनके बीच लगने वाला गुरुत्वाकर्षण बल होगा:
= (6.67 × 10⁻¹¹ × 200) / 4 = 3.34 × 10⁻⁹ N
यह बल बहुत छोटा होता है, इसलिए हमें दैनिक जीवन में इसका अनुभव नहीं होता।
निष्कर्ष:
- गुरुत्वाकर्षण बल सर्वत्र मौजूद है — यह ब्रह्माण्ड के प्रत्येक कण पर कार्य करता है।
- इस बल के कारण ही ग्रह सूर्य के चारों ओर, चंद्रमा पृथ्वी के चारों ओर घूमते हैं।
- यह बल वस्तुओं के भार, वर्षा और ज्वार-भाटा जैसी घटनाओं का कारण है।
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण का नियम बताता है कि —
हर वस्तु दूसरी वस्तु को आकर्षित करती है और यह बल द्रव्यमान के गुणनफल के समानुपाती तथा दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
उदाहरण प्रश्न
पृथ्वी का द्रव्यमान 6 × 10²⁴ kg है तथा चंद्रमा का द्रव्यमान 7.4 × 10²² kg है।
यदि पृथ्वी तथा चंद्रमा के बीच की दूरी 3.84 × 10⁵ km है, तो
पृथ्वी द्वारा चंद्रमा पर लगाए गए गुरुत्वाकर्षण बल की गणना कीजिए।
(दिया गया है: G = 6.7 × 10⁻¹¹ N·m²/kg²)
समाधान:
पृथ्वी का द्रव्यमान (m₁) = 6 × 10²⁴ kg
चंद्रमा का द्रव्यमान (m₂) = 7.4 × 10²² kg
दोनों के बीच की दूरी (r) = 3.84 × 10⁵ km = 3.84 × 10⁸ m
गुरुत्व नियतांक (G) = 6.7 × 10⁻¹¹ N·m²/kg²
सूत्र:
F = G × (m₁ × m₂) / r²
चरण 1 : दिए गए मानों को सूत्र में रखिए
F = (6.7 × 10⁻¹¹) × (6 × 10²⁴ × 7.4 × 10²²) / (3.84 × 10⁸)²
चरण 2 : गुणा और भाग की गणना
m₁ × m₂ = (6 × 7.4) × 10^(24 + 22) = 44.4 × 10⁴⁶ = 4.44 × 10⁴⁷
अब (r²) = (3.84 × 10⁸)² = 3.84² × 10¹⁶ = 14.75 × 10¹⁶ = 1.475 × 10¹⁷
चरण 3 : अब पूरे सूत्र में रखिए
F = (6.7 × 10⁻¹¹ × 4.44 × 10⁴⁷) / (1.475 × 10¹⁷)
F = (6.7 × 4.44 / 1.475) × 10^(⁻¹¹ + 47 − 17)
= (29.748 / 1.475) × 10¹⁹
≈ 20.17 × 10¹⁹
या, F ≈ 2.0 × 10²⁰ N
पृथ्वी द्वारा चंद्रमा पर लगाया गया गुरुत्वाकर्षण बल लगभग
2 × 10²⁰ न्यूटन है।
यह वही बल है जो चंद्रमा को पृथ्वी की परिक्रमा (orbit) में बनाए रखता है।
प्रश्नोत्तर
उत्तर:
संसार की प्रत्येक वस्तु दूसरी वस्तु को एक बल से अपनी ओर आकर्षित करती है,
जो उनके द्रव्यमानों के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
गणितीय रूप में –
F = G × (m₁ × m₂) / r²
जहाँ,
F = गुरुत्वाकर्षण बल,
G = सार्वत्रिक गुरुत्व नियतांक,
m₁ और m₂ = दोनों वस्तुओं के द्रव्यमान,
r = उनके बीच की दूरी।
उत्तर:
जब कोई वस्तु पृथ्वी की सतह पर रखी होती है, तो उसके और पृथ्वी के बीच लगने वाला गुरुत्वाकर्षण बल निम्न सूत्र से प्राप्त किया जाता है –
जहाँ,
F = पृथ्वी और वस्तु के बीच गुरुत्वाकर्षण बल,
G = सार्वत्रिक गुरुत्व नियतांक (6.67 × 10⁻¹¹ N·m²/kg²),
M = पृथ्वी का द्रव्यमान (6 × 10²⁴ kg),
m = वस्तु का द्रव्यमान,
R = पृथ्वी की त्रिज्या (6.4 × 10⁶ m)।
यही बल वस्तु का भार (Weight) कहलाता है।
अर्थात्, W = F = m × g जहाँ g = G×M/R²।
गुरुत्वाकर्षण के सार्वत्रिक नियम का महत्व
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण का नियम यह बताता है कि ब्रह्माण्ड की हर वस्तु दूसरी वस्तु को आकर्षित करती है।
यह नियम केवल पृथ्वी और वस्तुओं पर ही नहीं, बल्कि ग्रहों, उपग्रहों, तारों और आकाशगंगाओं पर भी लागू होता है।
इस नियम के कारण ही ब्रह्माण्ड का संतुलन और गति बनी रहती है।
- ग्रहों की गति को समझना: यह नियम बताता है कि ग्रह सूर्य के चारों ओर कैसे और क्यों घूमते हैं।
- चंद्रमा की परिक्रमा: पृथ्वी और चंद्रमा के बीच लगने वाला गुरुत्वाकर्षण बल ही चंद्रमा को पृथ्वी की कक्षा में बनाए रखता है।
- वर्षा और ज्वार-भाटा: गुरुत्वाकर्षण बल के कारण ही वर्षा की बूँदें नीचे गिरती हैं और समुद्र में ज्वार-भाटा (tides) उत्पन्न होते हैं।
- वस्तुओं का भार: वस्तुओं का भार वास्तव में पृथ्वी और वस्तु के बीच का गुरुत्वाकर्षण बल ही है।
- कृत्रिम उपग्रहों की गति: यह नियम कृत्रिम उपग्रहों की कक्षा (orbit) निर्धारण में सहायक है।
- ब्रह्माण्ड की संरचना का अध्ययन: तारों, ग्रहों और आकाशगंगाओं के बीच आकर्षण को समझने में यह नियम वैज्ञानिकों की सहायता करता है।
गुरुत्वाकर्षण का सार्वत्रिक नियम सम्पूर्ण ब्रह्माण्ड में वस्तुओं के आपसी आकर्षण और गति को समझाने वाला
एक मूलभूत और सार्वभौमिक नियम है। इसके बिना ग्रहों, उपग्रहों या आकाशगंगाओं की गति का अध्ययन संभव नहीं होता।
मुक्त पतन (Free Fall)
जब कोई वस्तु केवल पृथ्वी के गुरुत्वाकर्षण बल के प्रभाव में नीचे गिरती है और उस पर वायु प्रतिरोध (Air resistance) का प्रभाव नगण्य होता है, तो उस गति को मुक्त पतन (Free Fall) कहा जाता है।
अर्थात, जब कोई वस्तु ऊपर से गिराई जाती है और उस पर केवल पृथ्वी का गुरुत्वीय आकर्षण कार्य करता है, तो वस्तु समान रूप से त्वरण प्राप्त करती है। यह त्वरण गुरुत्वीय त्वरण (Acceleration due to gravity) कहलाता है।
महत्वपूर्ण तथ्य:
- मुक्त पतन के दौरान वस्तु की गति बढ़ती जाती है।
- गिरती वस्तु पर केवल एक बल कार्य करता है — पृथ्वी का गुरुत्वाकर्षण बल।
- यदि वायु प्रतिरोध को नज़रअंदाज कर दिया जाए, तो सभी वस्तुएँ समान गति से गिरेंगी, चाहे उनका द्रव्यमान कुछ भी हो।
मुक्त पतन में त्वरण (Acceleration in Free Fall)
मुक्त पतन में वस्तु को जो त्वरण प्राप्त होता है, उसे गुरुत्वीय त्वरण (g) कहा जाता है।
गुरुत्वीय त्वरण का सूत्र:
g = G × (M / R²)
जहाँ,
G = सार्वत्रिक गुरुत्वाकर्षण नियतांक (6.67 × 10⁻¹¹ N·m²/kg²)
M = पृथ्वी का द्रव्यमान (≈ 6 × 10²⁴ kg)
R = पृथ्वी की त्रिज्या (≈ 6.4 × 10⁶ m)
g = 9.8 m/s² (पृथ्वी की सतह पर)
निष्कर्ष:
मुक्त पतन का सिद्धांत यह दर्शाता है कि पृथ्वी का गुरुत्वाकर्षण बल सभी वस्तुओं को समान रूप से आकर्षित करता है।
इस सिद्धांत के कारण ही उपग्रहों की गति, प्रक्षेप्य गति और खगोलीय पिंडों की गति को समझना संभव हुआ है।
गुरुत्वीय त्वरण (g) के मान का परिकलन
जब कोई वस्तु पृथ्वी की सतह के पास मुक्त रूप से गिरती है, तो वह पृथ्वी के गुरुत्वाकर्षण बल के प्रभाव में त्वरण प्राप्त करती है। इस त्वरण को गुरुत्वीय त्वरण (Acceleration due to Gravity) कहा जाता है, जिसे g द्वारा प्रदर्शित किया जाता है।
व्युत्पत्ति (Derivation)
पृथ्वी द्वारा किसी वस्तु पर लगाया गया गुरुत्वाकर्षण बल न्यूटन के गुरुत्वाकर्षण के सार्वत्रिक नियम से प्राप्त किया जा सकता है:
F = G × (M × m) / R²
जहाँ,
G = सार्वत्रिक गुरुत्वाकर्षण नियतांक (6.67 × 10⁻¹¹ N·m²/kg²)
M = पृथ्वी का द्रव्यमान (6 × 10²⁴ kg)
m = वस्तु का द्रव्यमान
R = पृथ्वी की त्रिज्या (6.4 × 10⁶ m)
अब, पृथ्वी द्वारा वस्तु पर लगने वाला बल वस्तु के भार (Weight) के बराबर होता है —
F = m × g
इन दोनों समीकरणों को बराबर रखने पर:
m × g = G × (M × m) / R²
वस्तु का द्रव्यमान (m) दोनों ओर से कट जाएगा, अतः
g = G × (M / R²)
अब मान रखकर परिकलन करें:
G = 6.67 × 10⁻¹¹ N·m²/kg²
M = 6 × 10²⁴ kg
R = 6.4 × 10⁶ m
g = (6.67 × 10⁻¹¹ × 6 × 10²⁴) / (6.4 × 10⁶)²
g = (4.002 × 10¹⁴) / (4.096 × 10¹³)
g ≈ 9.77 m/s²
निष्कर्ष:
अतः पृथ्वी की सतह पर गुरुत्वीय त्वरण का मान लगभग 9.8 m/s² होता है। यह मान पृथ्वी के हर स्थान पर समान नहीं होता — ध्रुवों पर थोड़ा अधिक तथा विषुवत रेखा (Equator) पर थोड़ा कम होता है।
पृथ्वी के गुरुत्वीय बल के प्रभाव में वस्तुओं की गति
पृथ्वी के गुरुत्वाकर्षण बल के प्रभाव में किसी वस्तु की गति को समझने के लिए हम सामान्यतः वायु प्रतिरोध नगण्य मानते हैं।
ऐसी स्थितियों में गति पर सिर्फ एक स्थिर त्वरण g (नीचे की ओर) कार्य करता है। नीचे प्रमुख प्रकार और उनके संबंधित सूत्र दिए गए हैं — परीक्षा-उन्मुख और वेबसाइट-अनुकूल HTML स्वरूप में।
1. समान त्वरण वाली सीधी गिरावट (Uniformly accelerated straight fall / Free fall)
यदि किसी वस्तु को विशुद्ध रूप से गिराया जाता है (प्रारम्भिक वेग u = 0 या कोई आरम्भिक वेग u हो), तो वह नीचे की दिशा में समान त्वरण g पाएगी। मुख्य सूत्र:
- v = u + gt — समय t के पश्चात् चाल (v)। (नीचे की ओर गति को धनात्मक मानें तो +gt)
- s = ut + ½ g t² — t समय में गिरित दूरी (s)।
- v² = u² + 2 g s — चाल व दूरी का सम्बन्ध।
2. ऊर्ध्वमुख विक्षेपण (Vertical upward throw)
जब किसी वस्तु को ऊपर की दिशा में आरम्भिक वेग u से छोड़ा जाता है, तो गुरुत्वाकर्षण उसे धीरे-धीरे रोकेगा और परावर्तन (maximum height) पर इसकी ऊर्ध्वाधर चाल शून्य हो जाएगी।
- ऊपर की दिशा को + मानकर: चाल घटेगी: v = u − g t
- समय जब परावर्तन होगा: t₁ = u / g
- अधिकतम ऊँचाई: H = u² / (2 g)
- कुल समय (ऊपर और नीचे) = समयावधि (time of flight): T = 2u / g
3. प्रोजेक्टाइल मोशन (Projectile motion)
यदि किसी वस्तु को सतह के साथ θ कोण पर त्वरित वेग u से छोड़ा जाए, तो गति को दो स्वतंत्र घटकों में विभाजित किया जा सकता है — क्षैतिज (horizontal) और ऊर्ध्वाधर (vertical)। गुरुत्व केवल ऊर्ध्वरत भाग पर कार्य करता है।
- प्रारम्भिक क्षैतिज चाल: u_x = u cosθ
- प्रारम्भिक ऊर्ध्वाचल चाल: u_y = u sinθ
- समयावधि (Time of flight): T = (2 u sinθ) / g
- अधिकतम ऊँचाई (Maximum height): H = (u² sin²θ) / (2 g)
- क्षैतिज दूरी (Range): R = (u² sin 2θ) / g (जब लॉन्च और लैंडिंग की ऊँचाई समान हो)
- क्षैतिज गति: क्षैतिज दिशा में कोई त्वरण नहीं (वायु प्रतिरोध छोड़ा हो) ⇒ x = u cosθ · t
4. गुरुत्वाकर्षण के तहत वृत्तीय गति (Circular / Orbital motion – संक्षेप में)
यदि किसी पिंड को पृथ्वी के केन्द्र के परिमंडल के निकट कंसाच्या वेग के साथ रखा जाए ताकि केन्द्र की ओर आवश्यक तान्यात्मक (centripetal) त्वरण गुरुत्व द्वारा प्रदान हो, तो वह परिक्रमण कर सकता है। केन्द्राभिमुख त्वरण a_c = v² / r और उसे गुरुत्व द्वारा प्रदान किया जाना चाहिए: m v² / r = G M m / r² ⇒ परिक्रमण के लिए गतिवर्ग का निर्धारण।
5. सामान्य अवस्थाएँ और परीक्षा के लिए टिप्स
- उपर्युक्त सूत्रों में चिन्हों (signs) पर ध्यान दें — ऊपर को + माना हो तो गुरुत्व = −g।
- जब दूरी छोटी हो और g को स्थिर मानें तो उपर्युक्त सूत्र अच्छी तरह लागू होते हैं।
- वायु प्रतिरोध को अक्सर प्रश्न में छोड़ा गया माना जाता है — समस्या हल करते समय यह स्पष्ट कर लें।
- प्रोजेक्टाइल प्रश्नों में क्षैतिज और ऊर्ध्वाधर चालों को अलग-अलग रखें और समय को माध्यम बनाकर x तथा y निर्देशाओं के समीकरण जोड़ें।
छोटा उदाहरण (reference): यदि कोई वस्तु क्षैतिज वेग u = 20 m/s से 30° पर छोड़ी जाए और g = 9.8 m/s² हो, तो—
T = (2·20·sin30°)/9.8 = (40·0.5)/9.8 ≈ 2.04 s
R = (20²·sin60°)/9.8 ≈ (400·0.866)/9.8 ≈ 35.35 m
उदाहरण:
एक कार किसी कगार से गिरती है और 0.5 s में पृथ्वी की सतह पर पहुँचती है।
गुरुत्वीय त्वरण g = 10 m/s² मानते हुए, ज्ञात कीजिए—
- (i) धरती पर टकराते समय कार की चाल (v)
- (ii) 0.5 s के दौरान औसत चाल (v_avg)
समाधान:
मुक्त पतन में प्रारंभिक वेग u = 0 m/s है।
समान त्वरण g = 10 m/s² और समय t = 0.5 s दिया है।
(i) टकराते समय चाल: v = u + g t
(ii) औसत चाल: v_avg = (u + v) / 2
चरण 1: धरती पर टकराते समय चाल (v)
v = u + g t = 0 + (10 × 0.5) = 5 m/s
चरण 2: औसत चाल (v_avg)
v_avg = (u + v) / 2 = (0 + 5) / 2 = 2.5 m/s
(i) धरती पर टकराते समय कार की चाल ≈ 5 m/s
(ii) 0.5 s के दौरान औसत चाल ≈ 2.5 m/s
इस उदाहरण में देखा जा सकता है कि मुक्त पतन में वस्तु की चाल समय के साथ समान रूप से बढ़ती है और औसत चाल प्रारंभिक और अंतिम चाल का मध्य होता है।
प्रश्नोत्तर
उत्तर:
जब कोई वस्तु केवल पृथ्वी के गुरुत्वाकर्षण बल के प्रभाव में गिरती है और उस पर वायु प्रतिरोध नगण्य होता है, तो उस गिरावट को मुक्त पतन (Free Fall) कहते हैं।
इसमें वस्तु समान रूप से गुरुत्वीय त्वरण प्राप्त करती है और उसकी गति धीरे-धीरे बढ़ती है।
उत्तर:
पृथ्वी की सतह पर कोई वस्तु मुक्त रूप से गिरती है, तो उसे जो त्वरण प्राप्त होता है, उसे गुरुत्वीय त्वरण (Acceleration due to Gravity) कहते हैं।
यह त्वरण वस्तु के द्रव्यमान पर निर्भर नहीं करता और इसका मान पृथ्वी की सतह पर लगभग g ≈ 9.8 m/s² होता है।
यह बल ही वस्तु का भार (Weight) निर्धारित करता है।
द्रव्यमान (Mass)
द्रव्यमान किसी वस्तु में उपस्थित पदार्थ की मात्रा को कहते हैं।
यह वस्तु की गुरुत्वीय गुण और जड़त्व (Inertia) को दर्शाता है।
द्रव्यमान वस्तु के भार से अलग होता है। इसे सामान्यतः m द्वारा दर्शाया जाता है और इसका SI एकक किलोग्राम (kg) है।
मुख्य बिंदु:
- द्रव्यमान वस्तु की स्थायित्व (inertia) को मापता है।
- द्रव्यमान की मात्रा स्थान (location) पर निर्भर नहीं करती।
- द्रव्यमान और भार में अंतर है: भार गुरुत्वीय बल पर निर्भर करता है जबकि द्रव्यमान स्थिर रहता है।
भार और द्रव्यमान का सम्बन्ध:
पृथ्वी की सतह पर किसी वस्तु का भार (Weight) गुरुत्वीय बल द्वारा निर्धारित होता है।
संबंधित सूत्र:
जहाँ, W = भार (N), m = द्रव्यमान (kg), g = गुरुत्वीय त्वरण (≈9.8 m/s²)
इसका अर्थ यह है कि यदि किसी वस्तु का द्रव्यमान 1 kg है, तो उसका भार लगभग 9.8 N होगा।
द्रव्यमान और भार के बीच यह सरल संबंध गुरुत्वीय नियमों और मुक्त पतन की समझ के लिए आधार तैयार करता है।
भार (Weight)
किसी वस्तु पर पृथ्वी (या किसी ग्रह) का गुरुत्वाकर्षण बल कार्य करता है, उसी बल को हम भार (Weight) कहते हैं।
यह वस्तु के द्रव्यमान और गुरुत्वीय त्वरण पर निर्भर करता है।
भार को सामान्यतः W द्वारा दर्शाया जाता है और इसका SI एकक न्यूटन (N) है।
मुख्य बिंदु:
- भार गुरुत्वाकर्षण बल का ही प्रत्यक्ष माप है।
- भार वस्तु के द्रव्यमान पर निर्भर करता है।
- विभिन्न ग्रहों पर एक ही वस्तु का भार अलग होगा क्योंकि गुरुत्वीय त्वरण (g) अलग होगा।
- भूमि पर: W = m × g, जहाँ g ≈ 9.8 m/s²
उदाहरण:
यदि किसी वस्तु का द्रव्यमान m = 5 kg है और g = 10 m/s² मान लें, तो उसका भार होगा –
इस प्रकार, पृथ्वी पर यह वस्तु 50 न्यूटन के बल से गुरुत्वाकर्षित होती है।
ध्यान दें कि द्रव्यमान स्थिर रहता है, लेकिन भार गुरुत्वीय त्वरण के अनुसार बदल सकता है। उदाहरण के लिए, चंद्रमा पर g ≈ 1.6 m/s² होने के कारण वही वस्तु हल्की प्रतीत होगी।
किसी वस्तु का चंद्रमा पर भार
किसी वस्तु का भार उस ग्रह या उपग्रह के गुरुत्वाकर्षण बल पर निर्भर करता है।
चंद्रमा पर गुरुत्वीय त्वरण g_m ≈ 1.6 m/s² है, जो पृथ्वी के g ≈ 9.8 m/s² से बहुत कम है।
इसलिए, पृथ्वी पर भारी वस्तु चंद्रमा पर हल्की प्रतीत होती है।
सूत्र:
W_m = m × g_m
जहाँ,
W_m = चंद्रमा पर वस्तु का भार (N)
m = वस्तु का द्रव्यमान (kg)
g_m = चंद्रमा का गुरुत्वीय त्वरण (≈ 1.6 m/s²)
यदि किसी वस्तु का द्रव्यमान m = 10 kg है, तो उसका भार चंद्रमा पर होगा –
W_m = 10 × 1.6 = 16 N
यानी वही वस्तु पृथ्वी पर 98 N (10 × 9.8) होने के बावजूद, चंद्रमा पर केवल 16 N का भार अनुभव करेगी।
इस प्रकार, किसी ग्रह या उपग्रह पर वस्तु का भार उस स्थान के गुरुत्वीय त्वरण पर निर्भर करता है, जबकि द्रव्यमान हमेशा स्थिर रहता है।
उदाहरण: द्रव्यमान और भार
गुरुत्वीय त्वरण g ≈ 9.8 m/s² मानें।
वस्तु का भार W = m × g = 10 × 9.8 = 98 N
चंद्रमा पर गुरुत्वीय त्वरण g_m = 1.6 m/s² है।
इसका भार चंद्रमा की सतह पर ज्ञात कीजिए।
सबसे पहले वस्तु का द्रव्यमान ज्ञात करें:
m = W / g = 10 / 9.8 ≈ 1.02 kgचंद्रमा पर भार:
W_m = m × g_m = 1.02 × 1.6 ≈ 1.63 N
इस प्रकार, वही वस्तु पृथ्वी पर 10 N होने के बावजूद, चंद्रमा पर केवल लगभग 1.63 N का भार अनुभव करेगी।
यह उदाहरण दर्शाता है कि भार स्थान और गुरुत्वीय त्वरण पर निर्भर करता है, जबकि द्रव्यमान स्थिर रहता है।
प्रश्नोत्तर: द्रव्यमान और भार
उत्तर:
- द्रव्यमान (Mass): किसी वस्तु में उपस्थित पदार्थ की मात्रा को कहते हैं। यह वस्तु की जड़त्व (Inertia) और गुरुत्वीय गुण को दर्शाता है। इसे m द्वारा मापा जाता है और SI एकक kg है। द्रव्यमान किसी स्थान पर स्थिर रहता है।
- भार (Weight): किसी वस्तु पर गुरुत्वाकर्षण बल द्वारा लगाया गया बल। इसे W द्वारा मापा जाता है और SI एकक N है। भार स्थान पर निर्भर करता है (पृथ्वी, चंद्रमा आदि)।
- संबंधित सूत्र: W = m × g
उत्तर:
चंद्रमा पर गुरुत्वीय त्वरण g_m ≈ 1.6 m/s² है, जबकि पृथ्वी पर g ≈ 9.8 m/s² है।
वस्तु का भार गुरुत्वीय त्वरण पर निर्भर करता है। अतः चंद्रमा पर भार होगा –
इसलिए, किसी वस्तु का चंद्रमा पर भार पृथ्वी पर उसके भार का लगभग 1/6 होता है।
उदाहरण के लिए, यदि पृथ्वी पर कोई वस्तु 60 N भार की हो, तो चंद्रमा पर उसका भार ≈ 10 N होगा।
प्रणोद (Force) और दाब (Pressure)
1. प्रणोद (Force)
किसी वस्तु पर कार्य करने वाला वह बल जिसे वस्तु की गति बदलने, उसे स्थिर करने, आकार बदलने या दिशा बदलने के लिए प्रयुक्त किया जाता है, उसे प्रणोद (Force) कहते हैं।
न्यूटन के नियमों के अनुसार, यदि कोई वस्तु किसी बल के प्रभाव में होती है, तो उसकी गति या दिशा बदल सकती है।
प्रणोद का SI एकक न्यूटन (N) है।
मुख्य बिंदु:
- प्रणोद = द्रव्यमान × त्वरण (F = m × a)
- किसी वस्तु पर लगने वाला बल उसकी गति और दिशा को बदल सकता है।
- बल के प्रकार: गुरुत्वाकर्षण बल, घर्षण बल, चुंबकीय बल, आदि।
2. दाब (Pressure)
किसी सतह पर perpendicular दिशा में बल लगाने से सतह पर जो प्रभाव पड़ता है, उसे दाब (Pressure) कहते हैं।
दाब का SI एकक पस्कल (Pa) है, जहाँ 1 Pa = 1 N/m²।
सूत्र:
P = F / A
जहाँ,
P = दाब (Pa),
F = सतह पर लगने वाला बल (N),
A = बल लगने वाली सतह का क्षेत्रफल (m²)
उदाहरण:
- यदि 50 N बल 2 m² क्षेत्रफल पर लगाया जाए, तो दाब होगा P = 50 / 2 = 25 Pa।
- नुकीली वस्तुओं के नीचे दाब अधिक होता है क्योंकि क्षेत्रफल कम होता है।
इस प्रकार, प्रणोद किसी वस्तु को गति देने या बदलने वाला बल है, जबकि दाब उस बल का सतह पर प्रभाव मापता है।
एक लकड़ी का गुटका मेज पर रखा है।
- द्रव्यमान m = 5 kg
- विमाएँ = 40 cm × 20 cm × 10 cm
लकड़ी के टुकड़े द्वारा मेज पर लगने वाला दाब ज्ञात कीजिए, यदि यह निम्नलिखित सतहों पर रखा जाता है:
(a) 20 cm × 10 cm
(b) 40 cm × 20 cm
गुरुत्वीय त्वरण g = 10 m/s² मान लें।
समाधान:
दाब का सूत्र: P = F / A, जहाँ F = भार = m × g और A = सतह का क्षेत्रफल।
F = m × g = 5 × 10 = 50 N
(a) 20 cm × 10 cm = 0.2 m × 0.1 m = 0.02 m²
(b) 40 cm × 20 cm = 0.4 m × 0.2 m = 0.08 m²
(a) P = F / A = 50 / 0.02 = 2500 Pa
(b) P = F / A = 50 / 0.08 = 625 Pa
इस प्रकार, लकड़ी का गुटका जब छोटी सतह (20 cm × 10 cm) पर रखा जाता है तो दाब अधिक (2500 Pa) होता है और जब बड़ी सतह (40 cm × 20 cm) पर रखा जाता है तो दाब कम (625 Pa) होता है।
यह दिखाता है कि दाब सतह के क्षेत्रफल के प्रतिकूल होता है।
तरलों में दाब (Pressure in Liquids)
तरल पदार्थ (Liquid) किसी पात्र में होते हैं। किसी बिंदु पर तरल में दाब उस बिंदु पर तरल के ऊपर के द्रव्यमान और गुरुत्वीय बल पर निर्भर करता है।
तरलों में दाब हर दिशा में समान रूप से लागू होता है। यह सिद्धांत पाश्चात्य भौतिकी में पैसकलीय नियम (Pascal’s Law) कहलाता है।
सूत्र:
जहाँ,
P = तरल में दाब (Pa),
h = तरल की गहराई (m),
ρ = तरल का घनत्व (kg/m³),
g = गुरुत्वीय त्वरण (m/s²)।
मुख्य बिंदु:
- तरल में दाब गहराई के साथ बढ़ता है।
- दाब किसी दिशा में समान रूप से फैलता है।
- पात्र की आकृति या आकार का दाब पर कोई प्रभाव नहीं पड़ता।
- तरल के ऊपर कोई वस्तु रखें, तो भी दाब सिर्फ तरल की ऊँचाई और घनत्व पर निर्भर करता है।
उदाहरण:
P = h × ρ × g = 2 × 1000 × 10 = 20,000 Pa
इस प्रकार, तरलों में दाब सीधे तरल की गहराई और घनत्व पर निर्भर करता है। दाब की दिशा हमेशा सतत तरल के किसी भी बिंदु पर हर दिशा में समान होती है।
उत्प्लावकता (Buoyancy)
जब कोई वस्तु तरल या गैस में पूरी या आंशिक रूप से डुबाई जाती है, तो उस पर ऊपर की दिशा में एक बल लगता है, जिसे उत्प्लावक बल (Buoyant Force) कहते हैं।
इस बल के कारण वस्तु तरल में तैर सकती है या उसका वजन कम महसूस होता है। यह सिद्धांत आर्चिमिडीज का नियम (Archimedes’ Principle) कहलाता है।
आर्चिमिडीज का नियम:
“यदि कोई वस्तु तरल में पूरी या आंशिक रूप से डुबाई जाए, तो उस पर लगाया जाने वाला उत्प्लावक बल उस तरल द्वारा विस्थापित किए गए तरल के भार के बराबर होता है।”
सूत्र:
F_b = ρ × V × g
जहाँ,
F_b = उत्प्लावक बल (N)
ρ = तरल का घनत्व (kg/m³)
V = विस्थापित तरल का आयतन (m³)
g = गुरुत्वीय त्वरण (m/s²)
मुख्य बिंदु:
- उत्प्लावक बल हमेशा ऊपर की दिशा में कार्य करता है।
- यदि उत्प्लावक बल वस्तु के भार से अधिक है, तो वस्तु तरल की सतह पर तैरती है।
- यदि उत्प्लावक बल वस्तु के भार के बराबर है, तो वस्तु तरल में स्थिर रहती है।
- यदि उत्प्लावक बल वस्तु के भार से कम है, तो वस्तु डूब जाती है।
उदाहरण:
F_b = ρ × V × g = 1000 × 0.05 × 10 = 500 N
इस प्रकार, लकड़ी पर 500 N का बल ऊपर की दिशा में काम करेगा और इसे तैरने में मदद करेगा।
उत्प्लावकता का यह सिद्धांत जहाजों, डुबकी और अन्य तरल-संबंधित उपकरणों के डिज़ाइन में महत्वपूर्ण है।
प्रश्नोत्तर: वस्तुएँ पानी की सतह पर तैरती या डूबती क्यों हैं?
उत्तर:
जब कोई वस्तु पानी में डुबाई जाती है, तो उस पर ऊपर की दिशा में उत्प्लावक बल (Buoyant Force) कार्य करता है।
इस बल और वस्तु के भार (Weight) के अनुपात के आधार पर वस्तु तैरती या डूबती है:
- यदि उत्प्लावक बल = वस्तु का भार → वस्तु पानी में स्थिर रहती है।
- यदि उत्प्लावक बल > वस्तु का भार → वस्तु पानी की सतह पर तैरती है।
- यदि उत्प्लावक बल < वस्तु का भार → वस्तु पानी में डूब जाती है।
इसका मुख्य कारण आर्चिमिडीज का नियम (Archimedes’ Principle) है, जो बताता है कि तरल द्वारा विस्थापित तरल का भार ही उत्प्लावक बल निर्धारित करता है।
इसलिए हल्की और कम घनत्व वाली वस्तुएँ पानी पर तैरती हैं, जबकि भारी और उच्च घनत्व वाली वस्तुएँ डूब जाती हैं।
प्रश्नोत्तर: द्रव्यमान और तुला पर माप
उत्तर:
तुला पर जो माप दिखाई देती है वह आपका द्रव्यमान ही होती है।
इसलिए आपका द्रव्यमान वास्तव में 42 kg ही है।
तुला गुरुत्वीय बल को मापकर द्रव्यमान दर्शाती है, इसलिए यह सही माप है।
उत्तर:
तुला पर द्रव्यमान मापने का अर्थ है कि दोनों वस्तुओं में समान वजन है।
हालांकि, वास्तविकता में रुई का घनत्व कम और आयतन अधिक होता है, जबकि लोहे का घनत्व अधिक और आयतन कम होता है।
इसलिए, दोनों का द्रव्यमान तुला पर समान दिखेगा, लेकिन यदि हम केवल सघनता और आयतन देखें तो लोहे का टुकड़ा बहुत अधिक भारी और ठोस होता है।
रुई का बोरा हल्का लेकिन बड़ा होने के कारण तुला पर भी 100 kg दिखा सकता है।
मुख्य बिंदु:
- तुला पर दिखाया गया द्रव्यमान वस्तु की गुरुत्वीय प्रतिक्रिया पर आधारित होता है।
- वास्तविक घनत्व और आयतन देखकर वस्तु की “सघनता” और वास्तविक भौतिक गुणों का पता लगाया जा सकता है।
अभ्यास
उत्तर:
गुरुत्वाकर्षण बल का सूत्र: F = G * (m1 * m2) / r²
यदि r को आधा कर दिया जाए, तो F = G * (m1 * m2) / (r/2)² = G * (m1 * m2) / (r²/4) = 4 * (G * m1 * m2 / r²)
अर्थात बल चार गुना बढ़ जाएगा।
उत्तर:
गुरुत्वीय बल F = m × g
त्वरण a = F / m = (m × g) / m = g
इसलिए सभी वस्तुएँ, चाहे भारी हों या हल्की, समान त्वरण g से गिरती हैं।
इसमें हवा का प्रतिरोध न मानने पर सभी वस्तुएँ समान गति से गिरती हैं।
(पृथ्वी का द्रव्यमान 6 × 10²⁴ kg है तथा पृथ्वी की त्रिज्या 6.4 × 10⁶ m है)
उत्तर:
F = G * (m1 * m2) / r²
G = 6.7 × 10⁻¹¹ N·m²/kg², m1 = 6 × 10²⁴ kg, m2 = 1 kg, r = 6.4 × 10⁶ m
F = (6.7 × 10⁻¹¹ * 6 × 10²⁴ * 1) / (6.4 × 10⁶)²
F ≈ 9.8 N
अर्थात 1 kg वस्तु पर पृथ्वी का गुरुत्वीय बल ≈ 9.8 N होगा।
उत्तर:
गुरुत्वाकर्षण का नियम कहता है कि दो वस्तुएँ एक-दूसरे को समान और विपरीत बल से आकर्षित करती हैं।
इसलिए पृथ्वी और चंद्रमा पर लगने वाला बल बराबर है। (Newton’s Third Law)
उत्तर:
पृथ्वी का द्रव्यमान बहुत अधिक है, इसलिए वही बल लगने पर भी उसका त्वरण बहुत छोटा होता है।
त्वरण a = F / m, यहाँ m पृथ्वी का बहुत बड़ा होने के कारण a बहुत छोटा होता है।
इसलिए पृथ्वी की गति लगभग नगण्य होती है।
(i) एक वस्तु का द्रव्यमान दोगुना कर दिया जाए?
(ii) वस्तुओं के बीच की दूरी दोगुनी अथवा तीन गुनी कर दी जाए?
(iii) दोनों वस्तुओं के द्रव्यमान दोगुने कर दिए जाएँ?
उत्तर:
गुरुत्वाकर्षण बल F = G * (m1 * m2) / r²
(i) m1 दोगुना → F_new = G * (2 m1 * m2)/r² = 2F
(ii) दूरी r दोगुनी → F_new = G * (m1 * m2)/(2r)² = F / 4
दूरी r तीन गुनी → F_new = G * (m1 * m2)/(3r)² = F / 9
(iii) दोनों द्रव्यमान दोगुने → F_new = G * (2 m1 * 2 m2)/r² = 4F
उत्तर:
- सौरमंडल और ग्रहों की गति को समझना।
- तारामंडल, चंद्रमा, ग्रह और उपग्रहों की गति का अध्ययन।
- पृथ्वी पर वस्तुओं के गिरने और गुरुत्वीय बलों का परिकलन।
- सभी भौतिक घटनाओं में गुरुत्वीय बल की भूमिका समझना।
उत्तर:
मुक्त पतन की स्थिति में किसी वस्तु पर केवल पृथ्वी का गुरुत्वीय बल कार्य करता है।
इस समय वस्तु का त्वरण g कहलाता है।
पृथ्वी पर g ≈ 9.8 m/s²।
उत्तर:
पृथ्वी और किसी वस्तु के बीच का आकर्षण गुरुत्वीय बल (Gravitational Force) कहलाता है।
F = G * (M_earth * m_object) / R_earth²
उत्तर:
चूँकि ध्रुवों पर g का मान विषुवत वृत्त की तुलना में अधिक होता है, इसलिए उसी द्रव्यमान के सोने का भार (W = m × g) अधिक होगा।
यदि मित्र सोने को विषुवत वृत्त पर मापे, तो उसे कम भार दिखेगा।
इसलिए मित्र खरीदे गए सोने के भार से संतुष्ट नहीं होगा।
उत्तर:
सीधी कागज की शीट हवा के प्रतिरोध के कारण धीमी गिरती है।
मरोड़ कर बनाई गई गेंद में हवा का प्रतिरोध कम होता है और वह तेजी से गिरती है।
इससे स्पष्ट होता है कि वायुरोध (Air Resistance) गति को प्रभावित करता है।
उत्तर:
वस्तु का द्रव्यमान m = 10 kg
पृथ्वी पर g = 10 m/s² → W_earth = m × g = 10 × 10 = 100 N
चंद्रमा पर g_moon = g / 6 = 10 / 6 ≈ 1.67 m/s² → W_moon = 10 × 1.67 ≈ 16.7 N
(1) अधिकतम ऊँचाई जहाँ तक गेंद पहुँचती है।
(2) पृथ्वी की सतह पर वापस लौटने में लिया गया कुल समय।
उत्तर:
प्रारंभिक वेग u = 49 m/s, g = 9.8 ≈ 10 m/s²
अधिकतम ऊँचाई H:
v² = u² – 2 g H, जहाँ v = 0 m/s (ऊँचाई पर)
0 = 49² – 2 × 10 × H → H = 2401 / 20 ≈ 120.05 m
कुल समय T:
u = g × t (ऊपर जाने में समय) → t_up = 49 / 10 ≈ 4.9 s
कुल समय T = 2 × t_up ≈ 9.8 s
उत्तर:
u = 0 (छोड़ने पर), g = 10 m/s², s = 19.6 m
v² = u² + 2 g s = 0 + 2 × 10 × 19.6 = 392 → v = √392 ≈ 19.8 m/s
उत्तर:
अधिकतम ऊँचाई H:
v² = u² – 2 g H, v = 0
0 = 40² – 2 × 10 × H → H = 1600 / 20 = 80 m
नेट विस्थापन:
वापस पृथ्वी पर लौटने के बाद विस्थापन = 0 (चूँकि प्रारंभिक बिंदु पर लौटता है)
कुल दूरी:
उच्चतम बिंदु तक = 80 m, वापस = 80 m → कुल दूरी = 160 m
पृथ्वी का द्रव्यमान = 6 × 10²⁴ kg, सूर्य का द्रव्यमान = 2 × 10³⁰ kg, दूरी r = 1.5 × 10¹¹ m, G = 6.7 × 10⁻¹¹ N·m²/kg²
उत्तर:
F = G * (M_earth * M_sun) / r²
F = (6.7 × 10⁻¹¹) * (6 × 10²⁴ × 2 × 10³⁰) / (1.5 × 10¹¹)²
F = (6.7 × 10⁻¹¹ × 12 × 10⁵⁴) / (2.25 × 10²²)
F ≈ 80.4 × 10²¹ / 2.25 × 10²² ≈ 4.5 × 10²⁰ N
उत्तर:
पहला पत्थर: u₁ = 0, s₁ = 100 m, g = 10 m/s², नीचे की ओर गति → s₁(t) = 100 – 0.5 × 10 × t² = 100 – 5t²
दूसरा पत्थर: u₂ = 25 m/s, ऊपर की ओर, s₂(t) = 0 + 25t – 0.5 × 10 × t² = 25t – 5t²
मिलने की स्थिति: s₁ = s₂ → 100 – 5t² = 25t – 5t² → 100 = 25t → t = 4 s
स्थान: s = s₂ = 25×4 – 5×16 = 100 – 80 = 20 m ऊपर जमीन से।
(a) प्रारंभिक वेग, (b) अधिकतम ऊँचाई, (c) 4 s पश्चात् स्थिति।
उत्तर:
कुल समय T = 6 s → समय ऊपर जाने का t_up = 3 s (समय ऊपर = समय नीचे)
(a) प्रारंभिक वेग u = g × t_up = 10 × 3 = 30 m/s
(b) अधिकतम ऊँचाई H = 0.5 × u × t_up = u² / (2g) = 900 / 20 = 45 m
(c) 4 s पश्चात्: ऊपर जाने में 3 s, फिर 1 s नीचे → s = H – 0.5 g t² = 45 – 0.5×10×1² = 45 – 5 = 40 m ऊपर प्रारंभिक बिंदु
उत्तर:
उत्प्लावक बल हमेशा ऊपर की दिशा में कार्य करता है। यह वस्तु को तरल की सतह की ओर तैरने या वजन कम महसूस कराने में मदद करता है।
उत्तर:
प्लास्टिक का घनत्व पानी से कम होता है। पानी द्वारा विस्थापित तरल का भार उत्प्लावक बल प्रदान करता है।
चूंकि यह बल वजन से अधिक है, इसलिए गुटका ऊपर उठकर पानी की सतह पर तैरता है।
उत्तर:
पदार्थ का घनत्व ρ = m/V = 50/20 = 2.5 g/cm³
पानी का घनत्व 1 g/cm³ → ρ_p > ρ_water
अतः पदार्थ डूब जाएगा
उत्तर:
पैकेट का घनत्व ρ = m/V = 500/350 ≈ 1.43 g/cm³ > पानी का घनत्व 1 g/cm³ → पैकेट डूब जाएगा
विस्थापित पानी का आयतन = पैकेट का आयतन = 350 cm³
द्रव्यमान m_water = ρ_water × V = 1 × 350 = 350 g
गुरुत्वाकर्षण अध्याय के लिए उपयोगी Links:-
- NCERT Class 9 Science Chapter – गुरुत्वाकर्षण (PDF)
- BYJU’s – Class 9 Science: गुरुत्वाकर्षण समाधान
- Toppr – Gravity Chapter Notes & Examples
- LearnCBSE – गुरुत्वाकर्षण नोट्स
- Clear IIT Medical – Class 9 Science: Gravitation Chapter
Read more chapters:-