पाठ परिचय – प्रकाश का परावर्तन एवं अपवर्तन

कक्षा 10 विज्ञान अध्याय 10 – प्रकाश का परावर्तन एवं अपवर्तन हमारे चारों ओर घटित होने वाली प्रकाशीय घटनाओं को सरल भाषा में समझाने वाला एक महत्वपूर्ण पाठ है। इस अध्याय में आप जानेंगे कि प्रकाश का परावर्तन कैसे दर्पणों से टकराकर दिशा बदलता है और प्रकाश का अपवर्तन किस प्रकार एक माध्यम से दूसरे माध्यम में जाते समय झुक जाता है।

इसमें उत्तल और अवतल दर्पण, गोलीय दर्पणों के नियम, दर्पण सूत्र, लेंस सूत्र, आवर्धन, फोकस दूरी, अपवर्तक सूचकांक, और स्नेल का नियम जैसे महत्त्वपूर्ण विषयों को उदाहरणों के माध्यम से समझाया गया है।

यह लेख कक्षा 10 विज्ञान नोट्स हिंदी में तैयार करने, एनसीईआरटी विज्ञान समाधान पढ़ने और free MCQs practice करने वाले छात्रों के लिए अत्यंत उपयोगी है। साथ ही competitive exam preparation और हिंदी में विज्ञान समझने के लिए भी इसे अवश्य पढ़ें।

यहां दिए गए प्रश्नोत्तर, सूत्रों की व्याख्या, और रंगीन चार्ट आपकी तैयारी को और भी सटीक और रोचक बनाएंगे।

Table of Contents

प्रकाश क्या है? (What is Light?)

प्रकाश एक प्रकार की ऊर्जा है जो हमें वस्तुओं को देखने में सहायता करती है। जब प्रकाश किसी वस्तु पर पड़ता है और हमारी आँखों तक पहुँचता है, तभी हम उस वस्तु को देख पाते हैं। यह तरंगों के रूप में संचरित होता है और अत्यधिक वेग (लगभग 3×10⁸ मी./से.) से चलता है।

परिभाषा: प्रकाश वह ऊर्जा है जो वस्तुओं को दृश्यमान बनाती है और एक सीधी रेखा में संचरित होती है।

प्रकाश के गुण (Properties of Light)

क्रमांक	गुण	विवरण
1	सीधी रेखा में संचरण	प्रकाश हमेशा सीधी रेखा में चलता है, जब तक कि कोई बाधा न आए।
2	परावर्तन (Reflection)	प्रकाश किसी सतह से टकराकर वापस लौट सकता है, जैसे दर्पण से।
3	अपवर्तन (Refraction)	प्रकाश एक माध्यम से दूसरे माध्यम में जाने पर दिशा बदल लेता है।
4	गति	प्रकाश की गति निर्वात (vacuum) में लगभग 3×10⁸ m/s होती है।
5	ऊर्जा रूपांतरण	प्रकाश ऊर्जा को अन्य ऊर्जा जैसे ऊष्मा में बदला जा सकता है।

रोचक तथ्य: सूर्य का प्रकाश पृथ्वी तक पहुँचने में लगभग 8 मिनट 20 सेकंड लेता है।

प्रकाश का महत्त्व

हमें वस्तुओं को देखने में मदद करता है।
पौधों के लिए प्रकाश संश्लेषण में आवश्यक है।
जीवन के लिए ऊष्मा और ऊर्जा का स्रोत है।
प्रकाश की सहायता से दूरबीन, माइक्रोस्कोप, लेज़र आदि उपकरण काम करते हैं।

निष्कर्ष: प्रकाश जीवन और विज्ञान दोनों के लिए अत्यंत आवश्यक है। इसकी विभिन्न विशेषताओं को जानना, परावर्तन और अपवर्तन जैसे अध्यायों को समझने की नींव रखता है।

दीप्त और अदीप्त वस्तुएँ (Luminous and Non-Luminous Objects)

हम अपने चारों ओर अनेक वस्तुएँ देखते हैं, लेकिन वे हमें तभी दिखाई देती हैं जब वे या तो स्वयं प्रकाश उत्सर्जित करती हैं या किसी अन्य स्रोत से आने वाले प्रकाश को परावर्तित करती हैं। इसी आधार पर वस्तुओं को दो भागों में बाँटा गया है – दीप्त वस्तुएँ और अदीप्त वस्तुएँ।

1. दीप्त वस्तुएँ (Luminous Objects)

परिभाषा: वे वस्तुएँ जो स्वयं प्रकाश उत्पन्न करती हैं, दीप्त वस्तुएँ कहलाती हैं।

इन वस्तुओं को हम स्वयं से उत्पन्न प्रकाश के कारण देख पाते हैं।
ये प्रकाश का स्रोत होती हैं।

उदाहरण: सूर्य, दीपक, मोमबत्ती, टॉर्च, जलता हुआ बल्ब, जुगनू आदि।

2. अदीप्त वस्तुएँ (Non-Luminous Objects)

परिभाषा: वे वस्तुएँ जो स्वयं प्रकाश उत्पन्न नहीं करतीं, अदीप्त वस्तुएँ कहलाती हैं।

हम इन्हें तभी देख सकते हैं जब किसी अन्य दीप्त वस्तु का प्रकाश इन पर पड़े और वह हमारी आँखों तक परावर्तित हो।
ये प्रकाश के स्रोत नहीं होतीं।

उदाहरण: मेज़, कुर्सी, दीवार, पेड़, पुस्तक, मनुष्य आदि।

तुलनात्मक तालिका

मापदंड	दीप्त वस्तुएँ	अदीप्त वस्तुएँ
प्रकाश उत्पन्न करने की क्षमता	स्वयं प्रकाश उत्पन्न करती हैं	स्वयं प्रकाश उत्पन्न नहीं करतीं
दृश्यता	स्वयं के प्रकाश से दिखाई देती हैं	दूसरे स्रोत से आने वाले प्रकाश को परावर्तित कर दिखाई देती हैं
उदाहरण	सूर्य, बल्ब, जुगनू	पेड़, किताब, मनुष्य

निष्कर्ष: दीप्त वस्तुएँ प्रकाश का स्रोत होती हैं जबकि अदीप्त वस्तुएँ केवल प्रकाश को परावर्तित करके दृश्य होती हैं। प्रकाश का अध्ययन इन्हीं के व्यवहार पर आधारित है।

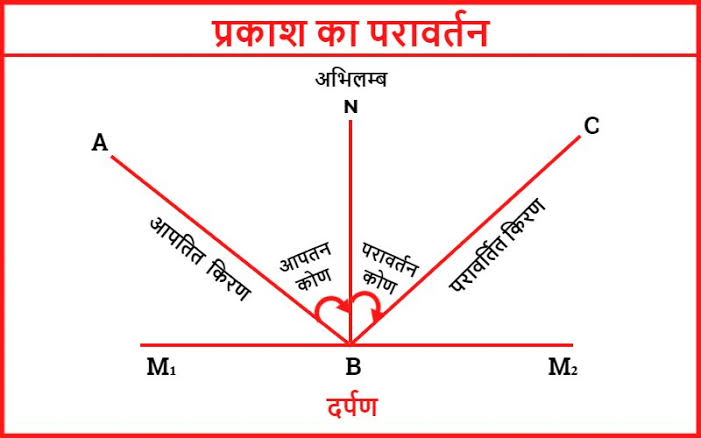
प्रकाश का परावर्तन (Reflection of Light)

जब प्रकाश की किरण किसी चमकदार और चिकनी सतह से टकराती है और अपने मार्ग को बदलते हुए वापस लौटती है, तो इस घटना को परावर्तन (Reflection) कहते हैं। यह परावर्तन हमें वस्तुओं को दर्पण में देखने, छवियाँ प्राप्त करने और प्रकाश की दिशा नियंत्रित करने में सहायता करता है।

परिभाषा: प्रकाश की किरण का किसी सतह से टकराकर उसी माध्यम में वापस लौटना परावर्तन कहलाता है।

परावर्तन के दो प्रमुख नियम (Laws of Reflection)

नियम	विवरण
पहला नियम	आपतित किरण (Incident Ray), परावर्तित किरण (Reflected Ray) और अभिलंब (Normal) सभी एक ही तल में होते हैं।
दूसरा नियम	आपतन कोण (Angle of Incidence) और परावर्तन कोण (Angle of Reflection) आपस में बराबर होते हैं। ∠i = ∠r

नियम

विवरण

पहला नियम

आपतित किरण (Incident Ray), परावर्तित किरण (Reflected Ray) और अभिलंब (Normal) सभी एक ही तल में होते हैं।

दूसरा नियम

आपतन कोण (Angle of Incidence) और परावर्तन कोण (Angle of Reflection) आपस में बराबर होते हैं।

∠i = ∠r

परावर्तन आरेख (Diagram Description)

किसी समतल दर्पण पर परावर्तन को दर्शाने के लिए एक आपतित किरण को दर्पण की सतह पर बनाएं। जहाँ वह टकराती है वहाँ एक लंबवत रेखा खींचते हैं जिसे Normal कहते हैं। इसके बाद परावर्तित किरण को उसी कोण पर दूसरी ओर बनाते हैं। आपतन कोण और परावर्तन कोण बराबर होते हैं।

ध्यान दें: परावर्तन की घटना दर्पणों, धातु की सतहों और पानी जैसे चमकदार सतहों पर देखी जा सकती है।

दर्पणों के प्रकार (Types of Mirrors)

दर्पण का प्रकार	विशेषताएँ	उदाहरण
समतल दर्पण (Plane Mirror)	चिकनी समतल सतह छवि सीधी, बराबर आकार की और उल्टी (laterally inverted)	घरों में, बाथरूम मिरर
अवतल दर्पण (Concave Mirror)	अंदर की ओर मुड़ी सतह छवि वास्तविक या आभासी, उल्टी या सीधी	दांतो के डॉक्टर, शेविंग मिरर
उत्तल दर्पण (Convex Mirror)	बाहर की ओर मुड़ी सतह छवि हमेशा आभासी, सीधी और छोटी	वाहनों के साइड मिरर

मुख्य तथ्य (Key Facts)

समतल दर्पण में छवि आभासी (Virtual), सीधी (Erect) और वास्तविक वस्तु के जितनी बड़ी होती है।
∠आपतन = ∠परावर्तन
उत्तल दर्पण का उपयोग पीछे का विस्तृत दृश्य देखने हेतु किया जाता है।

निष्कर्ष: परावर्तन प्रकाश की एक मौलिक विशेषता है जो हमें वस्तुओं को देखने, छवियाँ प्राप्त करने और विभिन्न प्रकाशीय यंत्रों के निर्माण में सहायता करता है।

गोलीय दर्पण (Spherical Mirrors)

वे दर्पण जिनकी परावर्तक सतह किसी गोले का भाग होती है, उन्हें गोलीय दर्पण कहा जाता है। इनकी सतह या तो अंदर की ओर झुकी होती है (अवतल) या बाहर की ओर निकली होती है (उत्तल)।

1. अवतल दर्पण (Concave Mirror)

परिभाषा: जिसकी परावर्तक सतह गोले की भीतर की ओर होती है, वह अवतल दर्पण कहलाता है। यह समारोहित (converging) दर्पण होता है।

प्रकाश किरणों को एक बिंदु पर समेटता है।
वास्तविक या आभासी, सीधी या उल्टी छवि बना सकता है।

उपयोग: शेविंग मिरर, दाँत चिकित्सक के उपकरण, सौर कुकर

2. उत्तल दर्पण (Convex Mirror)

परिभाषा: जिसकी परावर्तक सतह गोले की बाहरी ओर होती है, वह उत्तल दर्पण कहलाता है। यह विसरण (diverging) दर्पण होता है।

प्रकाश किरणों को फैलाता है।
हमेशा सीधी, आभासी और छोटी छवि बनाता है।

उपयोग: वाहनों के साइड मिरर, दुकानों की सुरक्षा दर्पणों में

गोलीय दर्पण के भाग (Parts of Spherical Mirror)

भाग	विवरण
ध्रुव (Pole) – P	दर्पण का मध्य बिंदु
घूर्ण केंद्र (Centre of Curvature) – C	उस गोले का केंद्र जिसका भाग दर्पण है
अक्ष (Principal Axis)	ध्रुव और घूर्ण केंद्र को जोड़ने वाली रेखा
मुख्य फोकस (Focus) – F	वे बिंदु जहाँ समानांतर किरणें परावर्तन के बाद मिलती या प्रतीत होती हैं
फोकस दूरी (Focal Length) – f	ध्रुव और फोकस के बीच की दूरी, f = R/2

मुख्य तथ्य (Key Facts)

अवतल दर्पण की फोकस दूरी धनात्मक होती है, यदि वस्तु सामने हो।
उत्तल दर्पण सदैव आभासी, सीधी और लघु छवि बनाता है।
अवतल दर्पण वास्तविक, उल्टी और कई आकार की छवियाँ बना सकता है, वस्तु की स्थिति पर निर्भर करता है।

निष्कर्ष: गोलीय दर्पण प्रकाश किरणों के दिशा परिवर्तन द्वारा छवियाँ उत्पन्न करते हैं और दैनिक जीवन में अनेक महत्त्वपूर्ण कार्यों में प्रयुक्त होते हैं।

गोलीय दर्पणों द्वारा प्रतिबिंब का बनना

जब प्रकाश की किरणें गोलीय दर्पण (अवतल या उत्तल) पर आपतित होती हैं, तो ये सतह परावर्तन के नियमों के अनुसार परावर्तित होकर छवि बनाती हैं। यह छवि वस्तु की स्थिति पर निर्भर करती है और उसकी प्रकृति, आकार एवं स्थिति अलग-अलग हो सकती है।

अवतल दर्पण द्वारा प्रतिबिंब

वस्तु की स्थिति	छवि की स्थिति	छवि की प्रकृति	छवि का आकार
अनंत पर	F (फोकस) पर	वास्तविक और उलटी	बिंदु जैसी
C के पार	C और F के बीच	वास्तविक और उलटी	छोटी
C पर	C पर	वास्तविक और उलटी	समान आकार
C और F के बीच	C के पार	वास्तविक और उलटी	बड़ी
F पर	अनंत पर	वास्तविक और उलटी	अनंत बड़ी
F और P (ध्रुव) के बीच	दर्पण के पीछे	आभासी और सीधी	बड़ी

उत्तल दर्पण द्वारा प्रतिबिंब

वस्तु की स्थिति	छवि की स्थिति	छवि की प्रकृति	छवि का आकार
किसी भी स्थिति में	दर्पण के पीछे	आभासी और सीधी	छोटी

महत्वपूर्ण तथ्य:

अवतल दर्पण वास्तविक और उलटी छवि बना सकता है, जबकि वस्तु बहुत पास हो तो आभासी और सीधी छवि भी बना सकता है।
उत्तल दर्पण हमेशा आभासी, सीधी और छोटी छवि बनाता है।
दर्पण सूत्र: 1/f = 1/v – 1/u (सभी दूरियाँ ध्रुव से मानी जाती हैं)
फोकस दूरी (f) = घूर्ण केंद्र (R) / 2

गोलीय दर्पणों के अनुप्रयोग

अवतल दर्पण का उपयोग – सौर कुकर, टॉर्च, वाहन के हैडलाइट, डेंटिस्ट के मिरर
उत्तल दर्पण का उपयोग – वाहनों के साइड मिरर, सड़क के मोड़ों पर चौकसी के लिए

निष्कर्ष: गोलीय दर्पण विभिन्न प्रकार की छवियाँ उत्पन्न कर सकते हैं, जो वैज्ञानिक एवं दैनिक जीवन दोनों में अत्यंत उपयोगी हैं।

किरण आरेखों का उपयोग करके गोलीय दर्पणों द्वारा बने प्रतिबिंबों का निरूपण

जब प्रकाश की किरणें किसी गोलीय दर्पण (अवतल या उत्तल) पर आपतित होती हैं, तो वे परावर्तन के नियमों का पालन करती हैं। इन परावर्तित किरणों के पथ को किरण आरेख (Ray Diagram) द्वारा दर्शाया जाता है जिससे हम यह निर्धारित कर सकते हैं कि प्रतिबिंब (Image) कहाँ और कैसे बनेगा।

किरण आरेख बनाने के नियम

मुख्य अक्ष के समांतर आने वाली किरण परावर्तित होकर फोकस (F) से गुजरती है।
फोकस से आने वाली किरण परावर्तित होकर मुख्य अक्ष के समांतर चली जाती है।
घूर्ण केंद्र से आने वाली किरण उसी पथ से लौट जाती है।
ध्रुव से टकराने वाली किरण, परावर्तन के सामान्य नियम (i = r) के अनुसार परावर्तित होती है।

1. अवतल दर्पण द्वारा प्रतिबिंब – किरण आरेख सहित सारणी

वस्तु की स्थिति	किरण आरेख में दिशा	प्रतिबिंब की स्थिति	प्रकृति
अनंत पर	मुख्य अक्ष के समांतर किरणें → परावर्तित होकर F से	F पर	वास्तविक, उलटी, अत्यंत छोटी
C से परे	एक किरण ‖ अक्ष, एक C की ओर	F और C के बीच	वास्तविक, उलटी, छोटी
C पर	एक किरण ‖ अक्ष, एक C की ओर	C पर	वास्तविक, उलटी, समान आकार
F और C के बीच	‖ अक्ष और F की ओर	C के पार	वास्तविक, उलटी, बड़ी
F पर	‖ अक्ष और F की ओर	अनंत पर	वास्तविक, बहुत बड़ी
F और P के बीच	‖ अक्ष और F की ओर	दर्पण के पीछे	आभासी, सीधी, बड़ी

2. उत्तल दर्पण द्वारा प्रतिबिंब

वस्तु की स्थिति	किरण आरेख में दिशा	प्रतिबिंब की स्थिति	प्रकृति
किसी भी दूरी पर	‖ अक्ष → परावर्तन के बाद ऐसा प्रतीत कि F से आ रही है	दर्पण के पीछे	आभासी, सीधी, छोटी

निष्कर्ष

किरण आरेख यह दिखाते हैं कि प्रकाश की किरणें दर्पण पर किस प्रकार परावर्तित होती हैं और कहां मिलती हैं या मिलती प्रतीत होती हैं। इससे हम प्रतिबिंब का स्थान, प्रकृति (वास्तविक/आभासी), दिशा (सीधी/उलटी), और आकार (बड़ा/छोटा) स्पष्ट रूप से समझ सकते हैं।

अवतल दर्पण के उपयोग

अवतल दर्पण (Concave Mirror) एक प्रकार का गोलीय दर्पण होता है जिसकी परावर्तक सतह अंदर की ओर वक्र होती है। यह दर्पण परावर्तित किरणों को एक बिंदु (फोकस) पर एकत्रित करता है, जिससे यह कई क्षेत्रों में उपयोगी बनता है। आइए इसके प्रमुख उपयोगों को समझें:

1. चिकित्सा क्षेत्र में

दंत चिकित्सक और ईएनटी विशेषज्ञ (नाक, कान, गला) अवतल दर्पण का उपयोग करते हैं ताकि रोगी के मुख, गले या कान की अंदरूनी सतह को बड़ा और स्पष्ट रूप से देखा जा सके।

2. वाहनों की हेडलाइट में

वाहनों की हेडलाइट में अवतल दर्पण का उपयोग किया जाता है क्योंकि यह प्रकाश की किरणों को एक दिशा में एकत्र कर फोकस करता है, जिससे आगे की सड़क पर तेज़ और सीधा प्रकाश पड़ता है।

3. सौर कुकर में

सोलर कुकर (Solar Cooker) में अवतल दर्पण का उपयोग सूर्य की किरणों को एक बिंदु पर केंद्रित करने के लिए किया जाता है, जिससे तापमान बढ़ता है और भोजन पकाया जा सकता है।

4. मेकअप और शेविंग मिरर

अवतल दर्पणों का उपयोग मेकअप मिरर या शेविंग मिरर के रूप में किया जाता है क्योंकि ये पास की वस्तुओं को बड़ा करके दिखाते हैं, जिससे चेहरे के बाल या फीचर्स को स्पष्ट देखा जा सकता है।

5. परावर्तक दूरबीनों में

रिफ्लेक्टिंग टेलीस्कोप (परावर्तक दूरबीन) में अवतल दर्पणों का उपयोग आकाशीय वस्तुओं से आने वाली किरणों को एकत्रित करके बड़ा और स्पष्ट प्रतिबिंब प्राप्त करने के लिए किया जाता है।

निष्कर्ष:

अवतल दर्पण अपनी प्रकाश-संकेन्द्रण क्षमता के कारण चिकित्सा, वैज्ञानिक उपकरणों, वाहनों, और घरेलू उपयोगों में अत्यंत उपयोगी होता है। यह छवि को बड़ा, स्पष्ट और फोकस्ड बना सकता है – यही इसकी खासियत है।

उत्तल दर्पण के उपयोग

उत्तल दर्पण (Convex Mirror) एक गोलीय दर्पण होता है जिसकी परावर्तक सतह बाहर की ओर उभरी होती है। यह दर्पण प्रकाश की किरणों को फैलाता है, जिससे यह छवि को छोटा, सीधा और आभासी बनाता है। इस विशेषता के कारण इसका उपयोग विभिन्न क्षेत्रों में किया जाता है।

1. वाहनों के साइड मिरर में

उत्तल दर्पण सबसे अधिक वाहनों के पीछे देखने वाले शीशों (साइड मिरर) में उपयोग होता है। यह बड़ा दृश्य क्षेत्र (wide field of view) प्रदान करता है, जिससे ड्राइवर को पीछे से आने वाले वाहनों की जानकारी मिलती है।

2. सड़क सुरक्षा के लिए मोड़ों पर

संकीर्ण और तीव्र मोड़ों (Blind Turns) पर उत्तल दर्पण लगाए जाते हैं ताकि दोनों ओर से आने वाले वाहन एक-दूसरे को देख सकें और दुर्घटनाएँ रोकी जा सकें।

3. सुरक्षा निगरानी में

बड़े शॉपिंग मॉल, स्टोर या बैंक जैसे स्थानों में उत्तल दर्पण का उपयोग सुरक्षा दृष्टि से किया जाता है। यह छिपे कोनों को देखने और चोरी रोकने में सहायक होता है।

4. संग्रहालयों और दीर्घाओं में

संग्रहालयों और दीर्घाओं में सुरक्षा और निगरानी के लिए उत्तल दर्पण लगाए जाते हैं, ताकि प्रत्येक कोने को कम कैमरों में भी देखा जा सके।

5. दृश्य क्षेत्र को बड़ा दिखाने के लिए

जहाँ अधिक दृश्यता की आवश्यकता होती है (जैसे ATM काउंटर या टोल प्लाज़ा), वहां उत्तल दर्पण का उपयोग किया जाता है ताकि कर्मचारियों को पूरा क्षेत्र एक नजर में दिखे।

निष्कर्ष:

उत्तल दर्पण हमेशा छोटी, सीधी और आभासी छवि बनाता है और अधिक क्षेत्र को कवर करता है, इसलिए यह सुरक्षा, निगरानी और ट्रैफिक नियंत्रण जैसे क्षेत्रों में अति उपयोगी है।

अभ्यास प्रश्नोत्तर – गोलीय दर्पण

1. अवतल दर्पण के मुख्य फोकस की परिभाषा लिखिए।

जब मुख्य अक्ष के समानांतर आने वाली सभी प्रकाश किरणें किसी अवतल दर्पण से परावर्तित होकर जिस बिंदु पर मिलती हैं, उसे उस दर्पण का मुख्य फोकस (Principal Focus) कहा जाता है। यह बिंदु दर्पण के ध्रुव और वक्रता केंद्र के बीच स्थित होता है।

2. एक गोलीय दर्पण की वक्रता त्रिज्या 20 cm है। इसकी फोकस दूरी क्या होगी?

गोलीय दर्पण की फोकस दूरी (f) और वक्रता त्रिज्या (R) के बीच संबंध होता है:

f = R / 2

अतः,
R = 20 cm ⇒ f = 20 / 2 = 10 cm

यदि यह अवतल दर्पण है तो f = -10 cm
यदि उत्तल दर्पण है तो f = +10 cm

3. उस दर्पण का नाम बताइए, जो बिंब का सीधा तथा आवर्धित प्रतिबिंब बना सके।

अवतल दर्पण ही ऐसा दर्पण है जो वस्तु को फोकस (F) और ध्रुव (P) के बीच रखने पर सीधा, आभासी तथा आवर्धित प्रतिबिंब बना सकता है। इसी कारण इसका उपयोग मेकअप मिरर और दंत चिकित्सा में होता है।

4. हम वाहनों में उत्तल दर्पण को पश्च-दृश्य दर्पण के रूप में वरीयता क्यों देते हैं?

हम उत्तल दर्पण को पश्च-दृश्य (Rear View) दर्पण के रूप में इसलिए वरीयता देते हैं क्योंकि:

• यह चौड़ा दृश्य क्षेत्र (wide field of view) प्रदान करता है।
• यह सीधा और छोटा प्रतिबिंब बनाता है, जिससे अधिक क्षेत्र कम स्थान में दिखाई देता है।
• इससे ड्राइवर को पीछे आने वाले वाहनों की जानकारी आसानी से मिल जाती है।

गोलीय दर्पणों द्वारा परावर्तन के लिए चिन्ह परिपाटी

गोलीय दर्पणों में परावर्तन के समय मापी जाने वाली सभी राशियों (जैसे दूरी, फोकस, आवर्धन आदि) के लिए एक निश्चित चिन्ह परिपाटी (Sign Convention) अपनाई जाती है। यह परिपाटी सभी गणनाओं को स्पष्ट एवं एकरूप बनाती है।

परावर्तन हेतु चिन्ह परिपाटी के नियम

सभी माप मुख्य अक्ष के सापेक्ष की जाती हैं।
मुख्य अक्ष के बाएं (left) दिशा में मापी गई दूरी को ऋणात्मक (−) लिया जाता है।
मुख्य अक्ष के दाएं (right) दिशा में मापी गई दूरी को धनात्मक (+) लिया जाता है।
मुख्य अक्ष के ऊपर की दिशा को धनात्मक (+) और नीचे की दिशा को ऋणात्मक (−) माना जाता है।
अवतल दर्पण में फोकस एवं वस्तु की दूरी ऋणात्मक होती है।
प्रतिबिंब यदि वास्तविक और उल्टा है तो उसकी ऊँचाई ऋणात्मक होती है।
यदि प्रतिबिंब आभासी और सीधा है तो उसकी ऊँचाई धनात्मक होती है।

संकेतों की सारणी

मापी गई राशि	धनात्मक कब	ऋणात्मक कब
वस्तु की दूरी (u)	–	सदैव (मुख्य अक्ष के बाईं ओर)
प्रतिबिंब की दूरी (v)	मुख्य अक्ष के दाईं ओर (उत्तल दर्पण में)	मुख्य अक्ष के बाईं ओर (अवतल में)
फोकस दूरी (f)	उत्तल दर्पण	अवतल दर्पण
प्रतिबिंब की ऊँचाई (h’)	सीधा प्रतिबिंब	उल्टा प्रतिबिंब
आवर्धन (M)	+ve → आभासी व सीधा	−ve → वास्तविक व उल्टा

निष्कर्ष:
चिन्ह परिपाटी गणितीय गणनाओं को स्पष्ट बनाती है और प्रतिबिंब की प्रकृति (सीधा/उल्टा, वास्तविक/आभासी) का पूर्वानुमान लगाने में सहायक होती है।

दर्पण सूत्र (Mirror Formula)

गोलीय दर्पणों के लिए, वस्तु की दूरी (u), प्रतिबिंब की दूरी (v) और फोकस दूरी (f) के बीच एक गणितीय संबंध होता है जिसे दर्पण सूत्र कहते हैं।

दर्पण सूत्र:

1/f = 1/v + 1/u

इस सूत्र में:

f = दर्पण की फोकस दूरी (focal length)
v = प्रतिबिंब की दूरी (image distance)
u = वस्तु की दूरी (object distance)

ध्यान देने योग्य बातें (चिन्ह परिपाटी):

वस्तु की दूरी (u) सदा ऋणात्मक (–) होती है।
अवतल दर्पण के लिए फोकस दूरी (f) ऋणात्मक होती है।
प्रतिबिंब की दूरी (v) वास्तविक प्रतिबिंब के लिए ऋणात्मक और आभासी प्रतिबिंब के लिए धनात्मक होती है।

उदाहरण:

एक अवतल दर्पण की फोकस दूरी −15 सेमी है। यदि एक वस्तु 30 सेमी दूरी पर रखी है, तो प्रतिबिंब की दूरी ज्ञात करें।

हल:

f = −15 cm, u = −30 cm

⇒ 1/f = 1/v + 1/u

⇒ 1/−15 = 1/v + 1/−30

⇒ −1/15 + 1/30 = 1/v

⇒ (−2 + 1)/30 = 1/v

⇒ −1/30 = 1/v

⇒ v = −30 cm

उत्तर: प्रतिबिंब 30 सेमी की दूरी पर वास्तविक और उल्टा बनेगा।

निष्कर्ष:
दर्पण सूत्र का प्रयोग करके हम आसानी से किसी भी गोलीय दर्पण में प्रतिबिंब की स्थिति और प्रकृति (आभासी/वास्तविक, सीधा/उल्टा) ज्ञात कर सकते हैं।

आवर्धन (Magnification)

जब किसी दर्पण द्वारा बना प्रतिबिंब वस्तु से बड़ा या छोटा दिखाई देता है, तो इसे आवर्धन कहते हैं। यह प्रतिबिंब की ऊँचाई और वस्तु की ऊँचाई के अनुपात से व्यक्त किया जाता है।

आवर्धन का सूत्र:

आवर्धन (M) = प्रतिबिंब की ऊँचाई / वस्तु की ऊँचाई = h’/h = −v/u

आवर्धन के संकेत (Signs of Magnification)

स्थिति	आवर्धन (M)	प्रतिबिंब की प्रकृति
M > 1	प्रतिबिंब बड़ा	आभासी और सीधा
M = 1	प्रतिबिंब बराबर	वास्तविक/आभासी
M < 1	प्रतिबिंब छोटा	वास्तविक और उल्टा
M < 0	ऋणात्मक	प्रतिबिंब वास्तविक व उल्टा
M > 0	धनात्मक	प्रतिबिंब आभासी व सीधा

निष्कर्ष:
आवर्धन बताता है कि दर्पण द्वारा बना प्रतिबिंब वस्तु की तुलना में कितना बड़ा या छोटा है और उसकी दिशा क्या है (सीधा/उल्टा)।

उदाहरण 1

प्रश्न: किसी ऑटोमोबाइल में पीछे का दृश्य देखने के लिए उपयोग होने वाले उत्तल दर्पण की वक्रता त्रिज्या 3.00 m है। यदि एक बस इस दर्पण से 5.00 m की दूरी पर स्थित है, तो प्रतिबिंब की स्थिति, प्रकृति तथा साइज़ ज्ञात कीजिए।

हल:

वक्रता त्रिज्या (R)	+3.00 m
बिंब-दूरी (u)	-5.00 m
फोकस दूरी (f)	+1.50 m

दर्पण सूत्र:
1/v + 1/u = 1/f
1/v = 1/f - 1/u = 1/1.5 - 1/(-5.0)
= 0.667 + 0.2 = 0.867
v = 1/0.867 ≈ 1.15 m

आवर्धन (m):
m = v/u = +1.15 / -5.00 = -0.23
=> प्रतिबिंब आभासी, सीधा और आकार में छोटा है।

उदाहरण 2

प्रश्न: कोई 4.0 cm साइज़ वाला पद्य किसी 15.0 cm फोकस दूरी के अवतल दर्पण से 25.0 cm दूरी पर रखा है। यह ज्ञात कीजिए कि पद्य को कितनी दूरी पर रखा जाए कि स्पष्ट प्रतिबिंब प्राप्त हो? प्रतिबिंब की प्रकृति तथा साइज़ ज्ञात कीजिए।

हल:

वस्तु ऊँचाई (h)	+4.0 cm
वस्तु दूरी (u)	-25.0 cm
फोकस दूरी (f)	-15.0 cm

दर्पण सूत्र:
1/v + 1/u = 1/f
1/v = 1/f - 1/u = 1/(-15) - 1/(-25) = (-5 + 3)/75 = -2/75
v = -37.5 cm

निष्कर्ष:
पद्य को 37.5 cm की दूरी पर रखना चाहिए जिससे प्रतिबिंब वास्तविक प्राप्त हो।

उदाहरण 1

प्रश्न: उस उत्तल दर्पण की फोकस दूरी ज्ञात कीजिए, जिसकी वक्रता त्रिज्या 32 cm है।

हल:

दिया गया: वक्रता त्रिज्या (R) = +32 cm
(उत्तल दर्पण के लिए R धनात्मक होता है)

सूत्र: फोकस दूरी (f) = R / 2

f = +32 / 2 = +16 cm

उत्तर: उत्तल दर्पण की फोकस दूरी +16 cm है।

उदाहरण 2

प्रश्न: कोई अवतल दर्पण आमने-सामने 10 cm की दूरी पर रखे किसी बिंब का तीन गुणा आवर्धित (बड़ा) वास्तविक प्रतिबिंब बनाता है। प्रतिबिंब दर्पण से कितनी दूरी पर है?

हल:

दिया गया:
वस्तु-दूरी (u) = –10 cm (सामने है इसलिए ऋणात्मक)
आवर्धन (m) = –3 (वास्तविक प्रतिबिंब के लिए आवर्धन ऋणात्मक)

सूत्र:
m = v/u
⇒ –3 = v / (–10)
⇒ v = +30 cm

उत्तर: प्रतिबिंब दर्पण से 30 cm की दूरी पर बनेगा।

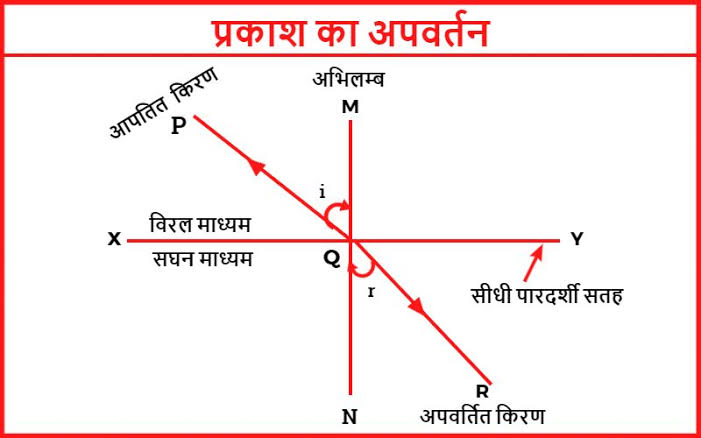
प्रकाश का अपवर्तन (Refraction of Light)

जब प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करता है, तो उसकी गति बदल जाती है, जिससे प्रकाश की दिशा मुड़ जाती है। इसी प्रक्रिया को प्रकाश का अपवर्तन कहा जाता है। यह एक महत्वपूर्ण भौतिक घटना है, जो अनेक प्राकृतिक एवं कृत्रिम परिघटनाओं में देखी जाती है, जैसे पानी में तिरती वस्तुएँ टेढ़ी दिखाई देना, लेंसों द्वारा प्रतिबिंब बनना आदि।

महत्वपूर्ण तथ्य:
जब प्रकाश एक घनत्व वाले माध्यम से दूसरे माध्यम में जाता है, तो उसकी चाल बदल जाती है और वह सामान्य रेखा की ओर या उससे दूर मुड़ जाता है। यही अपवर्तन कहलाता है।

अपवर्तन की परिभाषा:

प्रकाश का एक पारदर्शी माध्यम से दूसरे पारदर्शी माध्यम में जाने पर अपने पथ को बदलना प्रकाश का अपवर्तन कहलाता है।

अपवर्तन के कारण:

प्रकाश की गति माध्यम बदलने पर परिवर्तित होती है।
घनत्व में अंतर प्रकाश के दिशा परिवर्तन का कारण बनता है।

अपवर्तन में प्रकाश की दिशा:

स्थिति	प्रकाश की दिशा
कम घनत्व → अधिक घनत्व	सामान्य की ओर झुकता है
अधिक घनत्व → कम घनत्व	सामान्य से दूर झुकता है

स्नेल का नियम (Snell’s Law):

स्नेल के नियम के अनुसार:

n₁ sin i = n₂ sin r
जहाँ,
n₁ = पहले माध्यम का अपवर्तनांक
n₂ = दूसरे माध्यम का अपवर्तनांक
i = आपतन कोण
r = अपवर्तन कोण

अपवर्तन के दैनिक जीवन में उदाहरण:

जल में डूबा हुआ चम्मच मुड़ा हुआ दिखना
तारे टिमटिमाते हुए दिखते हैं
तैरते सिक्के की ऊँचाई अधिक दिखना

निष्कर्ष:
प्रकाश का अपवर्तन एक महत्वपूर्ण प्राकृतिक घटना है, जो हमें लेंस, दृष्टि सुधार यंत्र, चश्मे और विभिन्न ऑप्टिकल उपकरणों को समझने में मदद करती है।

काँच के आयताकार स्लैब से प्रकाश का अपवर्तन

जब प्रकाश की किरण हवा से काँच जैसे पारदर्शी आयताकार स्लैब में प्रवेश करती है, तो वह अपवर्तित हो जाती है। और जब वह काँच से पुनः हवा में प्रवेश करती है, तो फिर से अपवर्तन होता है। लेकिन यह बात महत्वपूर्ण है कि अंततः किरण अपने प्रारंभिक पथ के समानांतर बाहर निकलती है।

महत्वपूर्ण तथ्य:
काँच के स्लैब से गुजरने वाली प्रकाश किरण की दिशा दो बार बदलती है: एक बार जब वह स्लैब में प्रवेश करती है और दूसरी बार जब वह बाहर निकलती है। लेकिन अंतिम किरण, प्रारंभिक किरण के समानांतर होती है, केवल कुछ दूरी (lateral shift) से स्थानांतरित होती है।

अपवर्तन प्रक्रिया की व्याख्या

प्रकाश की किरण जब हवा से काँच में प्रवेश करती है (कम घनत्व → अधिक घनत्व), तो वह सामान्य की ओर मुड़ती है।
जब वह काँच से पुनः हवा में जाती है (अधिक घनत्व → कम घनत्व), तो वह सामान्य से दूर मुड़ती है।
अंततः, अंतिम अपवर्तित किरण, प्रारंभिक आपतित किरण के समानांतर होती है।

काँच स्लैब में आपतन और अपवर्तन

चरण	घटना	किरण की दिशा
1	हवा से काँच में प्रवेश	सामान्य की ओर
2	काँच से हवा में निकलना	सामान्य से दूर
3	अंतिम किरण	प्रारंभिक किरण के समानांतर

जानने योग्य तथ्य:
इस प्रकार की प्रक्रिया में किरण का पथ एक दिशा में थोड़ा खिसक जाता है, जिसे “lateral displacement” कहते हैं।

अपवर्तांक (Refractive Index)

जब प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करता है, तो उसकी दिशा बदल जाती है। इस दिशा परिवर्तन की मात्रा को मापने के लिए हम अपवर्तांक (Refractive Index) का प्रयोग करते हैं।

परिभाषा:
अपवर्तांक दो माध्यमों के बीच प्रकाश की चाल में हुए परिवर्तन का अनुपात है। यह यह दर्शाता है कि प्रकाश एक माध्यम से दूसरे माध्यम में प्रवेश करने पर कितनी गति से परिवर्तित होता है।

अपवर्तांक का गणितीय सूत्र

यदि किसी माध्यम में प्रकाश की चाल v हो और निर्वात (या वायु) में प्रकाश की चाल c हो, तो उस माध्यम का अपवर्तांक (n) इस प्रकार होगा:

सूत्र:

n = c / v

जहाँ,
n = माध्यम का अपवर्तांक
c = निर्वात में प्रकाश की चाल (≈ 3 × 10⁸ m/s)
v = माध्यम में प्रकाश की चाल

कुछ माध्यमों के अपवर्तांक

माध्यम	अपवर्तांक (n)
वायु	1.0003
पानी	1.33
काँच	1.5
हीरा	2.42

निष्कर्ष:
अपवर्तांक जितना अधिक होगा, उस माध्यम में प्रकाश की चाल उतनी ही धीमी होगी।

स्नेल का नियम (Snell’s Law)

जब प्रकाश एक पारदर्शी माध्यम से दूसरे माध्यम में प्रवेश करता है, तो वह अपने पथ को मोड़ लेता है। यह प्रक्रिया प्रकाश का अपवर्तन कहलाती है, और इस अपवर्तन की दिशा तथा कोण को नियंत्रित करने वाला नियम ही स्नेल का नियम है।

परिभाषा:
स्नेल का नियम कहता है कि दो माध्यमों की सतह पर प्रकाश के आपतन कोण और अपवर्तन कोण के साइन का अनुपात उनके संबंधित अपवर्तांकों के बराबर होता है।

स्नेल का गणितीय नियम:

सूत्र:

n₁ × sin i = n₂ × sin r

जहाँ,

n₁ = पहले माध्यम का अपवर्तांक
n₂ = दूसरे माध्यम का अपवर्तांक
i = आपतन कोण (angle of incidence)
r = अपवर्तन कोण (angle of refraction)

उदाहरण: हवा से पानी में प्रकाश का अपवर्तन

माध्यम	अपवर्तांक (n)	कोण
हवा	1.0003	i = 45°
पानी	1.33	r = ?

स्नेल का नियम लगाकर:

1 × sin 45° = 1.33 × sin r  
⇒ sin r = sin 45° / 1.33  
⇒ r ≈ 32°

निष्कर्ष:
स्नेल का नियम हमें अपवर्तन की दिशा और कोण की गणना करने में मदद करता है। यह ऑप्टिक्स, चश्मे, लेन्स और फाइबर ऑप्टिक तकनीक जैसे क्षेत्रों में अत्यंत उपयोगी है।

निरपेक्ष अपवर्तांक

प्रत्येक पारदर्शी माध्यम का एक निरपेक्ष अपवर्तांक (Absolute Refractive Index) होता है, जो यह दर्शाता है कि निर्वात (या वायु) की तुलना में उसमें प्रकाश की चाल कितनी कम हो जाती है। नीचे 20 प्रमुख पदार्थों के निरपेक्ष अपवर्तांक दिए गए हैं:

क्रमांक	पदार्थ	निरपेक्ष अपवर्तांक (n)
1	वायु (Air)	1.0003
2	पानी (Water)	1.33
3	बर्फ (Ice)	1.31
4	अल्कोहल (Alcohol)	1.36
5	ग्लिसरिन (Glycerin)	1.47
6	काँच (Glass – सामान्य)	1.5
7	क्राउन ग्लास (Crown Glass)	1.52
8	फ्लिंट ग्लास (Flint Glass)	1.62
9	क्वार्ट्ज (Quartz)	1.54
10	तेल (Oil)	1.47
11	पारा (Mercury)	1.62
12	कार्बन डाइसल्फाइड	1.63
13	एक्रेलिक (Plastic)	1.49
14	सिलिका (Silica)	1.46
15	नायलॉन (Nylon)	1.53
16	सफायर (Sapphire)	1.77
17	डायमंड (Diamond)	2.42
18	सिरमिक (Ceramic)	1.5
19	लीड ग्लास	1.7
20	क्लोरीन गैस	1.0008

ध्यान दें:
निरपेक्ष अपवर्तांक को केवल माध्यम में प्रकाश की चाल के आधार पर ही मापा जाता है। इसका कोई मात्रक नहीं होता।

प्रकाश के अपवर्तन पर आधारित महत्त्वपूर्ण प्रश्न

1. वायु में गमन करती प्रकाश की एक किरण जल में तिरछी प्रवेश करती है। क्या प्रकाश किरण अभिलंब की ओर झुकेगी अथवा अभिलंब से दूर हटेगी? बताइए क्यों?

जब प्रकाश वायु (कम अपवर्तनांक) से जल (अधिक अपवर्तनांक) में प्रवेश करता है, तो उसकी चाल घट जाती है और वह अभिलंब की ओर झुकती है।

कारण: अपवर्तन में प्रकाश की चाल अधिक घनत्व वाले माध्यम में कम हो जाती है, जिससे किरण का पथ अभिलंब की ओर मुड़ जाता है।

2. प्रकाश वायु से 1.50 अपवर्तनांक की काँच की प्लेट में प्रवेश करता है। काँच में प्रकाश की चाल कितनी है? निर्वात में प्रकाश की चाल 3 × 10⁸ m/s है।

दिया गया:
n = 1.50
c = 3 × 10⁸ m/s

सूत्र:
n = c / v ⇒ v = c / n

गणना:
v = (3 × 10⁸) / 1.5 = 2 × 10⁸ m/s

अतः काँच में प्रकाश की चाल 2 × 10⁸ मीटर/सेकंड है।

3. सारणी 9.3 से अधिकतम प्रकाशिक घनत्व के माध्यम को ज्ञात कीजिए। न्यूनतम प्रकाशिक घनत्व के माध्यम को भी ज्ञात कीजिए।

उत्तर:

अधिकतम प्रकाशिक घनत्व: हीरा (Diamond) — अपवर्तनांक 2.42
न्यूनतम प्रकाशिक घनत्व: वायु (Air) — अपवर्तनांक 1.0003

अतः हीरा सबसे अधिक प्रकाश को धीमा करता है जबकि वायु में प्रकाश की चाल सबसे तेज़ होती है।

4. आपको किरोसिन, तारपीन का तेल तथा जल दिए गए हैं। इनमें से किसमें प्रकाश सबसे अधिक तीव्र गति से चलता है? सारणी 9.3 में दिए गए आँकड़ों का उपयोग कीजिए।

अपवर्तांक (n):

किरोसिन = 1.44
तारपीन का तेल = 1.47
जल = 1.33

निष्कर्ष:
प्रकाश की गति अपवर्तांक के व्युत्क्रम के अनुपात में होती है, अतः जल में प्रकाश सबसे तेज़ गति से चलेगा क्योंकि उसका अपवर्तांक सबसे कम है।

5. हीरे का अपवर्तनांक 2.42 है। इस कथन का क्या अभिप्राय है?

इसका अर्थ है कि हीरे में प्रकाश की चाल, निर्वात की तुलना में 2.42 गुना धीमी हो जाती है।

गणितीय रूप में:
n = c / v ⇒ v = c / 2.42 ≈ 1.24 × 10⁸ m/s

अतः हीरे में प्रकाश की चाल काफ़ी कम होती है, जिससे उसमें अत्यधिक अपवर्तन होता है। यही कारण है कि हीरा इतनी अधिक चमक उत्पन्न करता है।

गोलीय लेंस द्वारा अपवर्तन

गोलीय लेंस वे पारदर्शी माध्यम होते हैं जिनकी एक या दोनों सतहें वक्र होती हैं। जब प्रकाश किरणें एक माध्यम से दूसरे माध्यम में प्रवेश करती हैं, तो उनकी दिशा बदल जाती है – इसी प्रक्रिया को अपवर्तन (Refraction) कहा जाता है। गोलीय लेंस इस अपवर्तन का उपयोग करके प्रकाश किरणों को फोकस करने या फैलाने में सहायक होते हैं।

महत्वपूर्ण तथ्य:
➤ गोलीय लेंस दो प्रकार के होते हैं: उत्तल लेंस (Convex) और अवतल लेंस (Concave)।
➤ लेंस द्वारा अपवर्तन के कारण प्रतिबिंब बनता है, जो वास्तविक या आभासी हो सकता है।
➤ लेंस का मुख्य अक्ष (Principal Axis) वह रेखा होती है जो लेंस के केंद्र से होकर जाती है।

गोलीय लेंस के प्रकार

लेंस का प्रकार	संरचना	प्रभाव
उत्तल लेंस (Convex Lens)	दोनों सतह बाहर की ओर उभरी हुई	संग्राही (Converging) – किरणें एक बिंदु पर मिलती हैं
अवतल लेंस (Concave Lens)	दोनों सतह अंदर की ओर झुकी हुई	विसरित (Diverging) – किरणें फैल जाती हैं

अपवर्तन की प्रक्रिया

जब प्रकाश की किरणें एक लेंस में प्रवेश करती हैं, तो वे हवा से काँच में जाकर धीमी हो जाती हैं, जिससे वे मुड़ जाती हैं। यदि लेंस उत्तल है, तो यह किरणों को अंदर की ओर मोड़कर एक बिंदु पर केंद्रित करता है। यदि लेंस अवतल है, तो यह किरणों को बाहर की ओर मोड़ता है और किरणें पीछे जाकर मिलती हुई प्रतीत होती हैं।

उत्तल लेंस का उपयोग: आवर्धक काँच, कैमरा, प्रोजेक्टर, मानव नेत्र
अवतल लेंस का उपयोग: निकट दृष्टिदोष (Myopia) के चश्मे, लेज़र यंत्रों में

लेंस से संबंधित प्रमुख परिभाषाएँ

लेंस प्रकाश के अपवर्तन से संबंधित एक महत्त्वपूर्ण यंत्र है, जिसका प्रयोग प्रतिबिंब निर्माण, चश्मों, कैमरों, तथा वैज्ञानिक उपकरणों में होता है। नीचे लेंस से संबंधित सभी मुख्य भागों की परिभाषाएँ दी गई हैं:

1. लेंस (Lens)

एक पारदर्शी माध्यम की वह वस्तु जिसकी एक या दोनों सतहें वक्र होती हैं, जिससे वह प्रकाश की किरणों को अपवर्तित करता है।

2. उत्तल लेंस (Convex Lens)

ऐसा लेंस जिसकी दोनों सतहें बाहर की ओर उभरी होती हैं। यह एक संग्राही (converging) लेंस होता है जो प्रकाश किरणों को एक बिंदु पर केंद्रित करता है।

3. अवतल लेंस (Concave Lens)

ऐसा लेंस जिसकी सतहें अंदर की ओर झुकी होती हैं। यह एक विसरित (diverging) लेंस होता है जो प्रकाश किरणों को फैला देता है।

4. मुख्य अक्ष (Principal Axis)

लेंस के केंद्र से होकर जाने वाली काल्पनिक रेखा जो लेंस के दोनों वक्रित केंद्रों को जोड़ती है।

5. लेंस का केंद्र (Optical Centre)

लेंस के भीतर वह बिंदु जिससे होकर गुजरने वाली किरण बिना विचलित हुए सीधे आगे निकल जाती है।

6. वक्रता केन्द्र (Centre of Curvature)

वह बिंदु जो लेंस की गोल सतह के गोले के केंद्र का प्रतिनिधित्व करता है। उत्तल लेंस में दो वक्रता केन्द्र होते हैं।

7. वक्रता त्रिज्या (Radius of Curvature)

वक्रता केंद्र और लेंस की सतह के बीच की दूरी को वक्रता त्रिज्या कहा जाता है।

8. मुख्य फोकस (Principal Focus – F)

लेंस पर समानांतर रूप से आने वाली किरणें अपवर्तन के पश्चात जिस बिंदु पर मिलती (उत्तल लेंस) या जिससे प्रकट होती हैं (अवतल लेंस), उसे मुख्य फोकस कहते हैं।

9. फोकस दूरी (Focal Length – f)

मुख्य अक्ष पर लेंस के केंद्र (O) और मुख्य फोकस (F) के बीच की दूरी को फोकस दूरी कहते हैं।

10. वास्तविक और आभासी प्रतिबिंब

जब प्रकाश की किरणें वास्तव में मिलती हैं तो वास्तविक प्रतिबिंब बनता है। जब वे मिलती हुई प्रतीत होती हैं, तब आभासी प्रतिबिंब बनता है।

उत्तल लेंस द्वारा प्रतिबिंब बनना (Image Formation by Convex Lens)

जब किसी वस्तु से आने वाली किरणें उत्तल लेंस पर गिरती हैं, तो अपवर्तन के बाद वे एक निश्चित स्थान पर मिलती हैं और वहाँ एक प्रतिबिंब (Image) बनता है। यह प्रतिबिंब वस्तु की स्थिति पर निर्भर करता है।

उत्तल लेंस द्वारा प्रतिबिंब निर्माण की विभिन्न स्थितियाँ

क्रम	वस्तु की स्थिति	प्रतिबिंब की स्थिति	प्रतिबिंब का आकार	प्रतिबिंब का स्वरूप
1	अनंत पर	मुख्य फोकस F₂ पर	अत्यंत छोटा बिंदु	वास्तविक और उल्टा
2	अनंत और 2F₁ के बीच	2F₂ और F₂ के बीच	छोटा	वास्तविक और उल्टा
3	2F₁ पर	2F₂ पर	समान आकार	वास्तविक और उल्टा
4	F₁ और 2F₁ के बीच	2F₂ से परे	बड़ा	वास्तविक और उल्टा
5	F₁ पर	अनंत पर	अत्यंत बड़ा	वास्तविक और उल्टा
6	F₁ और लेंस के बीच	लेंस के उसी ओर	बड़ा	आभासी और सीधा

याद रखने योग्य तथ्य:

केवल अंतिम स्थिति (F₁ और लेंस के बीच) में प्रतिबिंब आभासी होता है।
अन्य सभी स्थितियों में प्रतिबिंब वास्तविक, उल्टा और स्क्रीन पर प्राप्त करने योग्य होता है।
प्रतिबिंब का आकार वस्तु की स्थिति पर निर्भर करता है।

अवतल लेंस द्वारा प्रतिबिंब बनना

अवतल लेंस (Concave Lens) एक विसरक (diverging) लेंस होता है, जो किसी वस्तु से आने वाली समांतर प्रकाश किरणों को फैलाता है। इन किरणों के पीछे बढ़ाने पर वे एक बिंदु से आती प्रतीत होती हैं। इस प्रकार, अवतल लेंस द्वारा बना प्रतिबिंब सदैव आभासी, सीधा एवं लघुतर (छोटा) होता है।

महत्वपूर्ण तथ्य:
✔️ अवतल लेंस हमेशा आभासी प्रतिबिंब बनाता है।
✔️ प्रतिबिंब सीधा होता है और वस्तु से छोटा होता है।
✔️ यह प्रतिबिंब लेंस के उसी ओर बनता है, जहाँ वस्तु रखी होती है।

अवतल लेंस द्वारा प्रतिबिंब निर्माण की स्थिति

वस्तु की स्थिति	प्रतिबिंब की स्थिति	प्रतिबिंब का आकार	प्रतिबिंब का स्वरूप
किसी भी स्थिति में (अनंत पर, 2F, F या पास)	लेंस के उसी ओर, F₁ और O के बीच	छोटा (लघुतर)	आभासी और सीधा

उदाहरण:

यदि किसी वस्तु को अवतल लेंस के 10 cm दूरी पर रखा जाए, तो इसका प्रतिबिंब लेंस के उसी ओर बनेगा, जिसकी लंबाई वस्तु से कम होगी। यह आभासी होगा और सीधा दिखाई देगा।

लेंस सूत्र और आवर्धन (Lens Formula & Magnification)

जब किसी वस्तु से निकलने वाली किरणें लेंस से होकर गुजरती हैं, तो वे अपवर्तित होकर एक प्रतिबिंब बनाती हैं। प्रतिबिंब की स्थिति और आकार ज्ञात करने के लिए हम लेंस सूत्र और आवर्धन सूत्र का प्रयोग करते हैं।

🔹 लेंस सूत्र (Lens Formula)

लेंस सूत्र:

1/f = 1/v - 1/u

यहाँ,
f = लेंस की फोकस दूरी (cm)
v = प्रतिबिंब की दूरी (cm)
u = वस्तु की दूरी (cm)

नोट: सभी मात्राएँ साइन कन्वेंशन के अनुसार ली जाती हैं।

🔹 आवर्धन सूत्र (Magnification)

आवर्धन (M) =

h₂ / h₁ = v / u

जहाँ,
h₂ = प्रतिबिंब की ऊँचाई
h₁ = वस्तु की ऊँचाई
v = प्रतिबिंब की दूरी
u = वस्तु की दूरी

महत्वपूर्ण:
✔️ M > 1: प्रतिबिंब बड़ा है
✔️ M = 1: प्रतिबिंब और वस्तु समान आकार के हैं
✔️ M < 1: प्रतिबिंब छोटा है
✔️ +M: प्रतिबिंब सीधा है
✔️ -M: प्रतिबिंब उल्टा है

याद रखने योग्य बिंदु

उत्तल लेंस की फोकस दूरी धनात्मक होती है
अवतल लेंस की फोकस दूरी ऋणात्मक होती है
वस्तु की दूरी सदा ऋणात्मक मानी जाती है
प्रकाश हमेशा बाएँ से दाएँ चलता है (मानक कन्वेंशन)

लेंस की क्षमता (Power of a Lens)

लेंस की क्षमता यह दर्शाती है कि वह प्रकाश किरणों को कितनी अधिक मुड़ाव (bending) प्रदान कर सकता है। इसे **डायॉप्टर (Dioptre)** में मापा जाता है। अधिक क्षमता वाला लेंस किरणों को अधिक मोड़ता है।

महत्वपूर्ण तथ्य:
✔️ लेंस की क्षमता फोकस दूरी पर निर्भर करती है।
✔️ उत्तल लेंस (Convex) की क्षमता धनात्मक होती है।
✔️ अवतल लेंस (Concave) की क्षमता ऋणात्मक होती है।
✔️ क्षमता को डायॉप्टर (D) में व्यक्त किया जाता है।

🔹 लेंस की क्षमता का सूत्र

Power (P) = 100 / f
[जब f को सेंटीमीटर में दिया गया हो]
या
P = 1 / f (in meters)

जहाँ,
P = लेंस की क्षमता (Dioptre में)
f = फोकस दूरी (meter में या cm में)

📘 उदाहरण:

यदि किसी उत्तल लेंस की फोकस दूरी +25 cm है, तो उसकी क्षमता होगी:
P = 100 / f = 100 / 25 = +4 D
(ध्यान दें कि + चिह्न दर्शाता है कि यह उत्तल लेंस है।)

🔸 डायॉप्टर की इकाई तालिका

माप	विवरण
1 डायॉप्टर (D)	1 मीटर फोकस दूरी वाले लेंस की क्षमता
+ डायॉप्टर	उत्तल (Convex) लेंस
− डायॉप्टर	अवतल (Concave) लेंस

नोट: यदि दो या अधिक लेंस पास-पास रखे जाते हैं तो उनकी कुल क्षमता:

P_total = P₁ + P₂ + P₃ + …

प्रकाशिक घनत्व और माध्यम की तुलना

किसी माध्यम की प्रकाश को अपवर्तित करने की क्षमता को उसके प्रकाशिक घनत्व द्वारा व्यक्त किया जाता है। यह द्रव्यमान घनत्व से भिन्न होता है।

🔹 प्रकाशिक सघन माध्यम वह होता है जिसका अपवर्तनांक अधिक हो।
🔹 प्रकाशिक विरल माध्यम वह होता है जिसका अपवर्तनांक कम हो।

जब प्रकाश विरल माध्यम से सघन माध्यम में प्रवेश करता है, तो इसकी चाल धीमी हो जाती है और यह अभिलंब की ओर झुकती है।
जब प्रकाश सघन माध्यम से विरल माध्यम में प्रवेश करता है, तो उसकी चाल तेज़ हो जाती है और वह अभिलंब से दूर हटती है।

यह सिद्धांत प्रकाश के अपवर्तन को समझने में अत्यंत महत्त्वपूर्ण है और स्नेल का नियम इसी पर आधारित होता है।

लेंसों की कुल क्षमता का सिद्धांत

अनेक प्रकाशिक यंत्रों (जैसे सूक्ष्मदर्शी, दूरदर्शी, कैमरा आदि) में कई लेंसों का संयोजन किया जाता है ताकि प्रतिबिंब अधिक आवर्धित और सुस्पष्ट बन सके।

🔹 जब कई लेंस एक-दूसरे के संपर्क में रखे जाते हैं, तो उनकी कुल क्षमता (P) उनके पृथक-पृथक क्षमताओं (P₁, P₂, P₃,…) का बीजगणितीय योग होता है।

कुल क्षमता का सूत्र:
P_total = P₁ + P₂ + P₃ + ...

उदाहरण: यदि दो लेंसों की क्षमताएँ क्रमशः +2.0 D और +0.25 D हैं, तो कुल क्षमता = +2.25 D

👓 चश्मा बनाने में, फोकस दूरी के स्थान पर क्षमताओं का उपयोग अधिक सुविधाजनक होता है। आँखों की जांच करते समय, लेंसों को संयोजित करके आवश्यक कुल क्षमता प्राप्त की जाती है।

अनुप्रयोग: लेंसों की क्षमताओं की योज्यता का लाभ उठाकर, अनेक ऑप्टिकल यंत्रों में दोष कम किए जाते हैं और छवियाँ अधिक स्पष्ट बनती हैं। इसका प्रयोग कैमरा लेंस, सूक्ष्मदर्शी और दूरदर्शी में होता है।

लेंस की क्षमता से संबंधित प्रश्न और उत्तर

1. किसी लेंस की 1 डाइऑप्टर क्षमता को परिभाषित कीजिए।

उत्तर:
जब किसी लेंस की फोकस दूरी 1 मीटर होती है, तब उसकी क्षमता 1 डाइऑप्टर होती है।अर्थात्, 1 डाइऑप्टर (D) = 1 मीटर फोकस दूरी वाला लेंसइससे अधिक फोकस दूरी वाले लेंस की क्षमता कम और कम दूरी वाले लेंस की क्षमता अधिक होती है।

2. कोई उत्तल लेंस किसी सुई का वास्तविक तथा उल्टा प्रतिबिंब उस लेंस से 50 cm दूर बनाता है। यह सुई लेंस के सामने कहाँ रखी है, यदि प्रतिबिंब उसी साइज का बन रहा है? लेंस की क्षमता ज्ञात कीजिए।

उत्तर:
प्रतिबिंब वास्तविक, उल्टा और उसी आकार का है,
इसका अर्थ है कि वस्तु और प्रतिबिंब दोनों लेंस से 2f दूरी पर हैं।इसलिए,
प्रतिबिंब की दूरी (v) = +50 cm
तो वस्तु की दूरी (u) = –50 cm
⇒ 2f = 50 cm ⇒ f = 25 cm = 0.25 mअब, लेंस की क्षमता P = 1 / f
⇒ P = 1 / 0.25 = 4 Dवस्तु की दूरी = 50 cm
लेंस की क्षमता = +4 डाइऑप्टर

3. 2 मीटर फोकस दूरी वाले किसी अवतल लेंस की क्षमता ज्ञात कीजिए।

उत्तर:
फोकस दूरी = –2 m (अवतल लेंस के लिए फोकस ऋणात्मक होता है)
P = 1 / f
⇒ P = 1 / (–2) = –0.5 Dइसलिए लेंस की क्षमता = –0.5 डाइऑप्टर

आपने क्या सीखा – प्रकाश परावर्तन तथा अपवर्तन

प्रकाश समतल सतहों में गमन करता प्रतीत होता है।
दर्पण तथा लेंस वस्तुओं के प्रतिबिंब बनाते हैं। बिंब की स्थिति के अनुसार प्रतिबिंब वास्तविक अथवा आभासी हो सकते हैं।
सभी पारदर्शी पदार्थ पूर्ण परावर्तन के नियमों का पालन करते हैं। अपवर्तन भी उपयुक्त नियमों का पालन करता है।
गोलीय दर्पणों तथा लेंसों के लिए नई रेखीय बिंब-परिपाटी अपनाई जाती है:1/v + 1/u = 1/f जहाँ,
u = वस्तु-दूरी,
v = प्रतिबिंब-दूरी,
f = फोकस दूरी।
किसी गोलीय दर्पण की वक्रता त्रिज्या उसकी फोकस दूरी की दो गुना होती है।
उत्तल दर्पण हमेशा आभासी, सीधा तथा छोटा प्रतिबिंब बनाते हैं।
वस्तु की ऊँचाई तथा प्रतिबिंब की ऊँचाई के अनुपात को आवर्धन कहते हैं।
प्रकाश का वेग निर्वात में 3 × 10⁸ m/s होता है।
सघन तथा विरल माध्यमों में प्रकाश की चाल भिन्न होती है।
स्नेल का नियम अपवर्तन को समझाने में सहायक है।
अपवर्तनांक n = c/v तथा n₂₁ = sin i / sin r

अभ्यास प्रश्न

निम्न में से कौन-सा पदार्थ लेंस बनाने के लिए प्रयुक्त नहीं किया जा सकता?उत्तर: (c) मिट्टी
किसी बिंब का अवतल दर्पण द्वारा बना प्रतिबिंब आभासी, सीधा तथा बिंब से बड़ा पाया गया। वस्तु की स्थिति कहाँ होनी चाहिए?उत्तर: (a) मुख्य फोकस तथा वक्रता केंद्र के बीच
किसी बिंब का वास्तविक तथा समान साइज का प्रतिबिंब प्राप्त करने के लिए बिंब को उत्तल लेंस के सामने कहाँ रखें?उत्तर: (a) लेंस के मुख्य फोकस पर
यदि किसी वस्तु को उत्तल लेंस से 15 cm दूर रखा जाए और लेंस की फोकस दूरी 10 cm हो, तो प्रतिबिंब कहाँ बनेगा?

उत्तर: यह गणना द्वारा हल किया जाएगा:1/f = 1/v – 1/u ⇒ 1/10 = 1/v – 1/(-15)⇒ 1/v = 1/10 – 1/15 = (3–2)/30 = 1/30

⇒ v = 30 cm (आभासी प्रतिबिंब, लेंस की ओर)

प्रकाश – परावर्तन तथा अपवर्तन: अभ्यास प्रश्नों के उत्तर

प्रश्न 1:

निम्न में से कौन-सा पदार्थ लेंस बनाने के लिए प्रमुख नहीं किया जा सकता?

उत्तर: (c) मिट्टी
व्याख्या: मिट्टी अपारदर्शी होती है, जिससे प्रकाश पार नहीं हो पाता।

प्रश्न 2:

किसी बिंब का अवतल दर्पण द्वारा बना प्रतिबिंब आपाती, सीधा तथा बिंब से बड़ा पाया गया। वस्तु की स्थिति कहाँ होनी चाहिए?

उत्तर: (a) मुख्य फोकस तथा वक्रता केंद्र के बीच
व्याख्या: जब वस्तु मुख्य फोकस और वक्रता केंद्र के बीच होती है, तो प्रतिबिंब बड़ा, सीधा व आभासी होता है।

प्रश्न 3:

किसी उत्तल लेंस के सामने बिंब को इस प्रकार रखें कि वह वास्तविक तथा समान आकार का बने।

उत्तर: (a) लेंस के मुख्य फोकस पर
व्याख्या: वस्तु को 2F दूरी पर रखने पर बिंब भी उसी दूरी पर बनता है और आकार समान होता है।

प्रश्न 4:

फोकस दूरी -15 cm है, कौन-से दर्पण हो सकते हैं?

उत्तर: (a) दोनों अवतल
व्याख्या: अवतल दर्पण की फोकस दूरी ऋणात्मक होती है।

प्रश्न 5:

दर्पण व लेंस दोनों पर लागू होता है, यह कथन:

उत्तर: (d) या तो समतल अथवा उत्तल
व्याख्या: परावर्तन एवं अपवर्तन दोनों प्रकार के दर्पण एवं लेंस पर निर्भर करते हैं।

प्रश्न 6:

छोटे अक्षरों को पढ़ने के लिए किस प्रकार का लेंस उचित होगा?

उत्तर: (c) 5 cm फोकस दूरी का एक उत्तल लेंस
व्याख्या: उत्तल लेंस आवर्धन करता है।

प्रश्न 7:

किसी वस्तु का सीधा प्रतिबिंब उत्पन्न करना हो तो कौन-सा लेंस उपयुक्त है?

उत्तर: उत्तल लेंस जिसकी दूरी मुख्य फोकस से कम हो।

प्रश्न 8:

निम्नलिखित दृष्टियों को स्पष्ट रूप से देखने हेतु लेंसों का प्रयोग बताइए:

उत्तर: (c) सिरा वही (Hypermetropia)
व्याख्या: दीर्घदृष्टि दोष के लिए उत्तल लेंस का प्रयोग किया जाता है।

प्रश्न 9:

उत्तल लेंस का आधा भाग काले कागज से ढक दिया जाए तो क्या पूर्ण प्रतिबिंब बनेगा?

उत्तर: हाँ, परंतु प्रतिबिंब धुंधला होगा क्योंकि केवल आधे लेंस से प्रकाश अपवर्तित होगा।

प्रश्न 10:

5 cm लंबा वस्तु 10 cm फोकस दूरी वाले उत्तल लेंस के सामने 25 cm पर रखा गया है।

उत्तर:
u = -25 cm, f = +10 cm
Lens Formula: 1/v – 1/u = 1/f
1/v + 1/25 = 1/10 → v = 16.67 cm
आवर्धन: h’/h = v/u = 16.67/-25 = -0.667
प्रतिबिंब: वास्तविक, उल्टा, छोटा।

प्रश्न 11:

10 cm दूर पर रखी वस्तु 15 cm फोकस दूरी वाले अवतल लेंस के सामने:

उत्तर:
f = -15 cm, u = -10 cm
1/v – 1/u = 1/f
1/v + 1/10 = -1/15 → v = -6 cm
प्रतिबिंब: आभासी, सीधा, छोटा।

प्रश्न 12:

u = -10 cm, f = -15 cm → v = -6 cm (जैसा कि ऊपर हल किया गया)।

प्रश्न 13:

समतल दर्पण → प्रतिबिंब का आकार वस्तु के बराबर होता है, आभासी और सीधा होता है।

प्रश्न 14:

वृत्तीय अवतल दर्पण द्वारा 30 cm दूरी पर रखा गया वस्तु का बिंब 20 cm पर बनता है:

u = -30 cm, v = -20 cm
Lens Formula: 1/f = 1/v – 1/u = -1/20 + 1/30 = -1/60
f = -60 cm, Nature: वास्तविक, उल्टा, छोटा।

प्रश्न 15:

उत्तल दर्पण द्वारा बनी छवि 27 cm पर दिखाई देती है। वस्तु दर्पण से 30 cm पर रखी है।

u = -30 cm, v = +27 cm
Mirror Formula: 1/f = 1/v + 1/u
f = (27×-30)/(27-30) = -810/-3 = +270 cm
दर्पण की फोकस दूरी = 270 cm

प्रश्न 16:

फोकस दूरी = -50 cm, P = 100/f = -2 D
अवतल लेंस की क्षमता ऋणात्मक होती है।

प्रश्न 17:

यदि लेंस की क्षमता +1.5 D है, तो:

f = 100/P = 100/1.5 = 66.67 cm
लेंस उत्तल है क्योंकि क्षमता धनात्मक है।