Table of Contents

अध्याय 9 : बल तथा गति के नियम (Laws of Motion)

परिचय : हमारे चारों ओर अनेक वस्तुएँ गतिशील हैं — जैसे चलती हुई कार, गिरता हुआ फल, उड़ता हुआ पक्षी, या घूमता हुआ पंखा। कभी-कभी ये वस्तुएँ अपनी गति में परिवर्तन करती हैं, तो कभी स्थिर रहती हैं। क्या आपने कभी सोचा है कि किसी वस्तु की गति या दिशा क्यों बदलती है? इसका कारण है — बल (Force)।

इस अध्याय में हम जानेंगे कि बल क्या है, यह वस्तुओं की गति को कैसे प्रभावित करता है, और इसके पीछे कौन से न्यूटन के नियम कार्य करते हैं। सर आइज़क न्यूटन ने गति से संबंधित तीन प्रमुख नियम दिए, जो आज भी भौतिकी (Physics) के आधार स्तंभ माने जाते हैं।

रोचक तथ्य: सर आइज़क न्यूटन ने अपने गति के नियम 1687 ई. में प्रस्तुत किए थे। उन्होंने बताया कि किसी वस्तु पर जब तक कोई बाहरी बल नहीं लगता, वह अपनी अवस्था (विश्राम या समान वेग से गति) को बनाए रखती है।

बल (Force) क्या है?

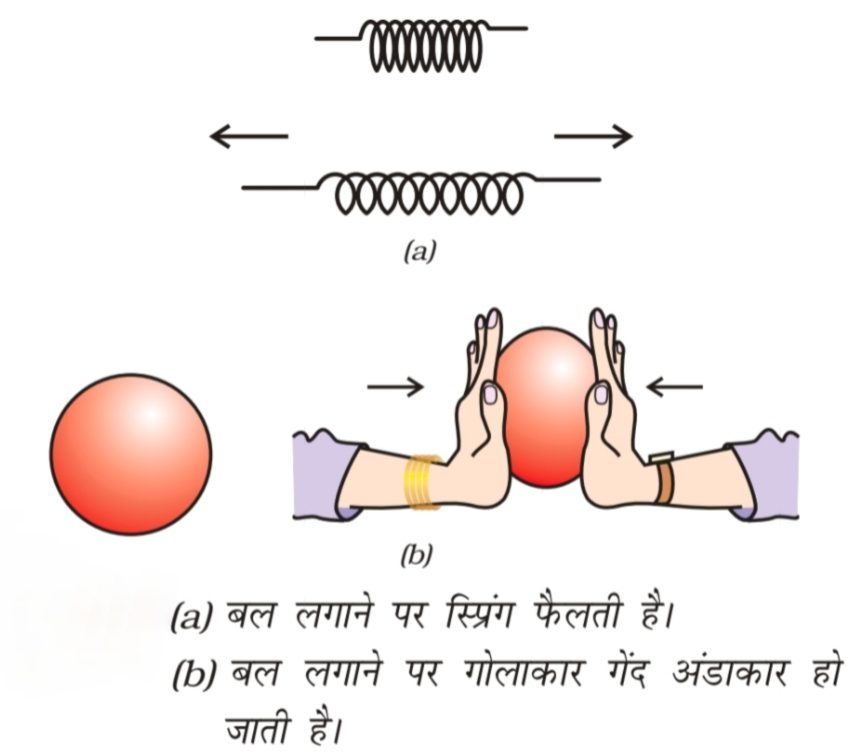
किसी वस्तु की अवस्था या उसकी गति में परिवर्तन लाने वाली क्रिया को बल कहा जाता है। बल से वस्तु की दिशा, गति या आकार में परिवर्तन हो सकता है।

बल के प्रभाव	उदाहरण
गति की अवस्था में परिवर्तन	रुकती हुई गेंद को लात मारने पर वह फिर चलने लगती है।
आकार में परिवर्तन	स्प्रिंग या रबर को खींचने या दबाने पर उसका आकार बदल जाता है।

ध्यान दें: बल एक सदिश राशि (Vector Quantity) है, अर्थात् इसमें परिमाण और दिशा दोनों होती हैं।

न्यूटन के गति के तीन नियम (Newton’s Laws of Motion)

नियम	विवरण	उदाहरण
पहला नियम (जड़त्व का नियम)	कोई वस्तु तब तक विश्राम या समान वेग से चलती रहेगी जब तक उस पर कोई बाहरी बल न लगाया जाए।	चलती बस के अचानक रुकने पर यात्री आगे की ओर झुक जाता है।
दूसरा नियम	वस्तु का त्वरण लगाए गए बल के समानुपाती और द्रव्यमान के व्युत्क्रमानुपाती होता है। (F = m × a)	कम द्रव्यमान वाली वस्तु को समान बल से अधिक गति मिलती है।
तीसरा नियम	हर क्रिया के बराबर और विपरीत दिशा में एक प्रतिक्रिया होती है।	बंदूक चलाने पर गोली आगे जाती है और बंदूक पीछे की ओर झटकती है।

सारांश: न्यूटन के ये तीनों नियम हमें यह समझने में मदद करते हैं कि किसी वस्तु की गति कैसे और क्यों बदलती है। ये नियम दैनिक जीवन की अनेक घटनाओं जैसे चलना, दौड़ना, वाहन चलाना आदि में लागू होते हैं।

संतुलित एवं असंतुलित बल (Balanced and Unbalanced Forces)

जब किसी वस्तु पर एक से अधिक बल लगाए जाते हैं, तो वे बल वस्तु की गति या अवस्था को प्रभावित कर सकते हैं। वस्तु की गति बदलेगी या नहीं — यह इस बात पर निर्भर करता है कि लगाए गए बल आपस में संतुलित हैं या असंतुलित।

मुख्य विचार:
किसी वस्तु की गति में परिवर्तन तभी होता है जब उस पर लगाए गए बल आपस में संतुलित न हों। अर्थात् असंतुलित बल ही वस्तु की गति को बदलते हैं।

(1) संतुलित बल (Balanced Forces)

जब किसी वस्तु पर लगने वाले सभी बलों का योगफल शून्य होता है, तो ऐसे बलों को संतुलित बल कहा जाता है। ये बल वस्तु की गति या दिशा में कोई परिवर्तन नहीं लाते।

विशेषता	विवरण
बलों का योगफल	शून्य (0)
गति पर प्रभाव	वस्तु की गति या दिशा में कोई परिवर्तन नहीं होता।
आकार पर प्रभाव	वस्तु के आकार में परिवर्तन हो सकता है।

उदाहरण:

टेबल पर रखी किताब पर गुरुत्वाकर्षण बल उसे नीचे की ओर खींचता है और मेज़ उतना ही बल ऊपर की ओर लगाती है — दोनों बल संतुलित हैं।
रस्सी खींचने का खेल (Tug of war) तब तक स्थिर रहता है जब तक दोनों दल समान बल लगाते हैं।

(2) असंतुलित बल (Unbalanced Forces)

जब किसी वस्तु पर लगने वाले बलों का योगफल शून्य नहीं होता, तो वे बल असंतुलित बल कहलाते हैं। असंतुलित बल वस्तु की गति या दिशा में परिवर्तन लाते हैं — अर्थात् वस्तु को गति देते हैं या रोक देते हैं।

विशेषता	विवरण
बलों का योगफल	शून्य नहीं
गति पर प्रभाव	वस्तु की गति, दिशा या आकार में परिवर्तन होता है।
कार्य करने की क्षमता	असंतुलित बल कार्य (Work) कर सकता है, क्योंकि यह गति उत्पन्न करता है।

उदाहरण:

रस्साकशी में यदि एक टीम अधिक बल लगाती है, तो रस्सी उसी दिशा में खिंचने लगती है — यह असंतुलित बल का प्रभाव है।
गाड़ी को धक्का देने पर जब असंतुलित बल लगता है, तो वह चलने लगती है।

सारांश:

संतुलित बलों का योग शून्य होता है और वे गति में परिवर्तन नहीं करते।
असंतुलित बलों का योग शून्य नहीं होता और वे वस्तु की गति या दिशा को बदलते हैं।
असंतुलित बल ही वस्तु को गति प्रदान करते हैं।

न्यूटन का प्रथम गति का नियम (Newton’s First Law of Motion)

सर आइज़क न्यूटन ने गति से संबंधित तीन नियम दिए। इनमें पहला नियम वस्तु की गति और विश्राम की अवस्था को समझाने में मदद करता है। इस नियम को जड़त्व का नियम (Law of Inertia) भी कहा जाता है।

नियम का कथन:

“कोई वस्तु तब तक विश्राम की अवस्था में या समान वेग से सीधी रेखा में गति करती रहेगी जब तक उस पर कोई बाहरी असंतुलित बल न लगाया जाए।”

इसका अर्थ है कि वस्तु की गति या दिशा तभी बदलेगी जब उस पर कोई असंतुलित बल कार्य करेगा। यदि कोई बल नहीं लगता, तो वस्तु अपनी वर्तमान अवस्था (विश्राम या समान गति) बनाए रखती है।

जड़त्व (Inertia) क्या है?

जड़त्व किसी वस्तु का वह गुण है जिसके कारण वह अपनी अवस्था (विश्राम या समान वेग से गति) को बनाए रखने का प्रयास करती है। जड़त्व का संबंध वस्तु के द्रव्यमान (mass) से होता है — जितना अधिक द्रव्यमान, उतना अधिक जड़त्व।

जड़त्व का प्रकार	विवरण	उदाहरण
विश्राम का जड़त्व (Inertia of Rest)	वस्तु अपनी विश्राम अवस्था को बनाए रखना चाहती है।	चलती बस के अचानक चलने पर यात्री पीछे की ओर झुक जाता है।
गति का जड़त्व (Inertia of Motion)	वस्तु अपनी गति की अवस्था को बनाए रखना चाहती है।	चलती बस के अचानक रुकने पर यात्री आगे की ओर झुक जाता है।
दिशा का जड़त्व (Inertia of Direction)	वस्तु अपनी गति की दिशा को बनाए रखना चाहती है।	मुड़ते समय वाहन के अंदर बैठे लोग एक ओर झुक जाते हैं।

उदाहरण:

टेबलक्लॉथ पर रखे बर्तन गिराए बिना कपड़ा खींचना — बर्तन अपने जड़त्व के कारण वहीं रहते हैं।
पेड़ को हिलाने पर सूखे पत्ते नीचे गिर जाते हैं क्योंकि उनका जड़त्व कम होता है।

वैज्ञानिक व्याख्या:

यदि कोई बल कार्य नहीं कर रहा, तो वस्तु अपनी अवस्था बनाए रखती है। वस्तु पर बल तभी प्रभाव डालता है जब वह असंतुलित हो। यही कारण है कि हमें किसी वस्तु को गति देने या रोकने के लिए बल लगाना पड़ता है।

सारांश:

प्रथम गति का नियम वस्तु के जड़त्व की व्याख्या करता है।
जब तक बाहरी असंतुलित बल नहीं लगता, वस्तु अपनी अवस्था नहीं बदलती।
जड़त्व वस्तु का प्राकृतिक गुण है जो उसके द्रव्यमान पर निर्भर करता है।

गैलीलियो गैलीली का परिचय

पूरा नाम: गैलीलियो गैलीली (Galileo Galilei)
जन्म: 15 फरवरी 1564 ई., पीसा (इटली)
मृत्यु: 8 जनवरी 1642 ई., आर्केट्री (इटली)
राष्ट्रीयता: इतालवी (Italian)
व्यवसाय: वैज्ञानिक, गणितज्ञ, खगोलशास्त्री, भौतिक विज्ञानी

प्रमुख योगदान:

गैलीलियो को “आधुनिक विज्ञान का जनक” कहा जाता है।
उन्होंने गति के नियमों और जड़त्व के सिद्धांत को स्पष्ट किया।
उन्होंने सबसे पहले दूरबीन का निर्माण किया और उससे चंद्रमा के गड्ढों तथा बृहस्पति के उपग्रहों की खोज की।
उन्होंने बताया कि वस्तुएँ समान गति से गिरती हैं, उनका भार इसका कारण नहीं होता।
उन्होंने सूर्यकेंद्रीय सिद्धांत (Heliocentric Theory) का समर्थन किया — जिसके अनुसार सूर्य ब्रह्मांड का केंद्र है, न कि पृथ्वी।

विज्ञान में योगदान:

जड़त्व का सिद्धांत: कोई वस्तु तब तक अपनी गति की अवस्था में बनी रहती है जब तक उस पर कोई बाहरी बल कार्य नहीं करता।
दोलन (Pendulum): उन्होंने पेंडुलम के समान काल गुण का अध्ययन किया।
दूरबीन से खोजें: चंद्रमा के पहाड़, बृहस्पति के चार उपग्रह, सूर्य के धब्बे।

उपाधियाँ:

आधुनिक भौतिकी का जनक
आधुनिक प्रेक्षणीय खगोलशास्त्र का जनक
वैज्ञानिक विधि (Scientific Method) के प्रवर्तक

प्रसिद्ध कथन:

“सत्य को नकारा जा सकता है, पर बदला नहीं जा सकता।”

जड़त्व तथा द्रव्यमान (Inertia and Mass)

जड़त्व (Inertia) किसी वस्तु की वह स्वाभाविक प्रवृत्ति है जिसके कारण वह अपनी गति या विश्राम की अवस्था को बनाए रखती है जब तक उस पर कोई बाहरी बल कार्य न करे।

अर्थात् — किसी वस्तु की गति में परिवर्तन करने के लिए बाहरी बल की आवश्यकता होती है। वस्तु स्वयं अपनी अवस्था नहीं बदल सकती।

उदाहरण:
1. जब चलती बस अचानक रुकती है तो यात्री आगे की ओर झुक जाते हैं।
2. जब स्थिर बस अचानक चलती है तो यात्री पीछे की ओर झुकते हैं।
3. मेज़ पर रखी किताब तब तक नहीं खिसकती जब तक उसे धक्का न दिया जाए।

जड़त्व के प्रकार

क्रम	जड़त्व का प्रकार	विवरण	उदाहरण
1.	विश्राम जड़त्व (Inertia of Rest)	किसी वस्तु की अपनी विश्राम अवस्था को बनाए रखने की प्रवृत्ति।	मेज़ पर रखी पुस्तक तब तक नहीं खिसकती जब तक उस पर बल न लगाया जाए।
2.	गति जड़त्व (Inertia of Motion)	किसी वस्तु की अपनी गति को बनाए रखने की प्रवृत्ति।	चलती बस के अचानक रुकने पर यात्री आगे की ओर झुकते हैं।
3.	दिशा जड़त्व (Inertia of Direction)	किसी वस्तु की अपनी गति की दिशा को बनाए रखने की प्रवृत्ति।	मोड़ पर मुड़ते समय वाहन के अंदर बैठे व्यक्ति बाहर की ओर झुक जाते हैं।

द्रव्यमान और जड़त्व का संबंध

जड़त्व का परिमाण किसी वस्तु के द्रव्यमान (Mass) पर निर्भर करता है। जितना अधिक द्रव्यमान होगा, उतना अधिक जड़त्व होगा।

उदाहरण:
एक ट्रक और एक साइकिल को समान बल से धक्का देने पर साइकिल जल्दी गति पकड़ लेती है जबकि ट्रक को गति देने के लिए अधिक बल की आवश्यकता होती है।
इसका कारण है कि ट्रक का द्रव्यमान अधिक होने से उसका जड़त्व भी अधिक होता है।

निष्कर्ष

इस प्रकार, जड़त्व किसी वस्तु की गति में परिवर्तन का विरोध करने की प्रवृत्ति है, और यह द्रव्यमान पर निर्भर करता है।

अभ्यास प्रश्न – जड़त्व तथा द्रव्यमान

प्रश्न 1.

निम्न में किसका जड़त्व अधिक है:

एक रबर की गेंद एवं उसी आकार का पत्थर
एक साइकिल एवं एक रेलगाड़ी
पाँच रुपये का एक सिक्का एवं एक रुपये का सिक्का

उत्तर:
जड़त्व द्रव्यमान पर निर्भर करता है। जिस वस्तु का द्रव्यमान अधिक होता है, उसका जड़त्व भी अधिक होता है।(a) पत्थर का जड़त्व रबर की गेंद से अधिक है।(b) रेलगाड़ी का जड़त्व साइकिल से अधिक है।(c) पाँच रुपये के सिक्के का जड़त्व एक रुपये के सिक्के से अधिक है।

प्रश्न 2.

नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास करें:
“फुटबॉल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।”

इसके साथ ही उस कारक की भी पहचान करें जो प्रत्येक अवस्था में बल प्रदान करता है।

उत्तर:
गेंद का वेग कुल तीन बार बदलता है —

पहली बार जब पहला खिलाड़ी गेंद को किक लगाता है।
दूसरी बार जब दूसरा खिलाड़ी गेंद को गोल की ओर किक करता है।
तीसरी बार जब गोलकीपर गेंद को पकड़कर वापस किक लगाता है।

प्रत्येक अवस्था में खिलाड़ी का पैर या गोलकीपर का हाथ गेंद पर बल प्रदान करता है जिससे गेंद का वेग बदलता है।

प्रश्न 3.

किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं। क्यों?

उत्तर:
जब पेड़ की शाखा को तीव्रता से हिलाया जाता है, तो शाखा के साथ-साथ शाखा से जुड़ी हुई टहनियाँ तो हिल जाती हैं, लेकिन पत्तियाँ अपने जड़त्व के कारण कुछ क्षण तक स्थिर रहने की प्रवृत्ति रखती हैं।
इस कारण पत्तियाँ शाखा से अलग होकर नीचे गिर जाती हैं।
अर्थात्: यह विश्राम जड़त्व (Inertia of Rest) का उदाहरण है।

प्रश्न 4.

जब कोई गतिशील बस अचानक रुकती है तो आप आगे की ओर झुक जाते हैं और जब विरामावस्था से गतिशील होती है तो पीछे की ओर हो जाते हैं, क्यों?

उत्तर:
जब बस अचानक रुकती है, तो शरीर का निचला भाग बस के साथ रुक जाता है, परंतु ऊपरी भाग जड़त्व के कारण आगे की ओर बढ़ने की प्रवृत्ति रखता है, जिससे व्यक्ति आगे की ओर झुक जाता है।
जब बस अचानक चलती है, तो शरीर का निचला भाग बस के साथ गति पकड़ लेता है, परंतु ऊपरी भाग अपने विश्राम की अवस्था बनाए रखता है, जिससे व्यक्ति पीछे की ओर झुक जाता है।
यह घटना भी जड़त्व (Inertia) का उदाहरण है।

गति का द्वितीय नियम (Newton’s Second Law of Motion)

न्यूटन का द्वितीय गति का नियम यह बताता है कि किसी वस्तु पर लगाया गया बल उसकी संवेग में परिवर्तन की दर के समानुपाती होता है और यह परिवर्तन लगाए गए बल की दिशा में होता है।

नियम का कथन:
“किसी वस्तु के संवेग (Momentum) में परिवर्तन की दर लगाए गए बल के समानुपाती होती है और यह परिवर्तन लगाए गए बल की दिशा में होता है।”

गणितीय रूप में

F ∝ (Δp / Δt)

यहाँ p = m × v (संवेग), अतः

F = m × a

जहाँ:
F = बल (Force)
m = द्रव्यमान (Mass)
a = त्वरण (Acceleration)

नियम का अर्थ

यदि किसी वस्तु पर अधिक बल लगाया जाए तो उसका त्वरण अधिक होगा।
यदि किसी वस्तु का द्रव्यमान अधिक है, तो समान बल पर उसका त्वरण कम होगा।
बल का कार्य संवेग में परिवर्तन उत्पन्न करना है।

समीकरण के अनुसार संबंध

परिमाण	संबंध
बल और त्वरण	बल सीधे अनुपाती है (F ∝ a)
बल और द्रव्यमान	बल द्रव्यमान और त्वरण दोनों पर निर्भर करता है
त्वरण और द्रव्यमान	त्वरण बल के समानुपाती तथा द्रव्यमान के व्युत्क्रमानुपाती होता है (a ∝ 1/m)

उदाहरण

उदाहरण 1: एक फुटबॉल खिलाड़ी गेंद को किक लगाता है। बल के कारण गेंद का संवेग बदलता है और वह तेज गति से आगे बढ़ती है।

उदाहरण 2: ट्रक और साइकिल पर समान बल लगाने पर साइकिल अधिक त्वरण प्राप्त करती है क्योंकि उसका द्रव्यमान कम होता है।

SI मात्रक

परिमाण	SI मात्रक
बल (Force)	न्यूटन (N)
द्रव्यमान (Mass)	किलोग्राम (kg)
त्वरण (Acceleration)	मीटर प्रति सेकंड² (m/s²)

1 न्यूटन बल की परिभाषा

जब 1 किलोग्राम द्रव्यमान वाली वस्तु को 1 मीटर/सेकंड² की दर से त्वरित करने के लिए बल लगाया जाता है, तब लगाए गए बल का परिमाण 1 न्यूटन कहलाता है।

अर्थात्: 1 N = 1 kg × 1 m/s²

निष्कर्ष

न्यूटन का द्वितीय नियम यह स्पष्ट करता है कि किसी वस्तु की गति में परिवर्तन (त्वरण) उत्पन्न करने के लिए बल आवश्यक है, और यह बल वस्तु के द्रव्यमान तथा प्राप्त त्वरण दोनों पर निर्भर करता है।

गति के द्वितीय नियम की गणितीय गणना (Mathematical Formulation of Second Law of Motion)

न्यूटन के गति के द्वितीय नियम के अनुसार, बल किसी वस्तु के संवेग में परिवर्तन की दर के समानुपाती होता है। अब हम इसे गणितीय रूप में समझते हैं।

मान लेते हैं:

वस्तु का द्रव्यमान = m
प्रारंभिक वेग = u
अंतिम वेग = v
समय = t
लगा हुआ बल = F

संवेग (Momentum):

किसी वस्तु का संवेग (p) उसके द्रव्यमान (m) और वेग (v) के गुणनफल के बराबर होता है।

संवेग (p) = m × v

अब परिवर्तन की दर ज्ञात करें:

प्रारंभिक संवेग = m × u
अंतिम संवेग = m × v

संवेग में परिवर्तन = (m × v) − (m × u)

संवेग में परिवर्तन = m(v − u)

यदि यह परिवर्तन समय t में होता है, तो परिवर्तन की दर होगी:

संवेग में परिवर्तन की दर = m(v − u) / t

द्वितीय नियम के अनुसार :

F ∝ संवेग में परिवर्तन की दर

या, F ∝ m(v − u)/t

समानुपाती चिन्ह हटाने के लिए एक स्थिरांक (k) लिया जाता है:

F = k × m(v − u)/t

SI इकाइयों में k = 1 माना जाता है, अतः

F = m(v − u)/t

चूंकि (v − u)/t = a (त्वरण), इसलिए

F = m × a

इससे स्पष्ट है कि :

बल वस्तु के द्रव्यमान और त्वरण दोनों पर निर्भर करता है।
अधिक द्रव्यमान या अधिक त्वरण से अधिक बल की आवश्यकता होती है।

निष्कर्ष:

न्यूटन का दूसरा नियम बताता है कि बल = द्रव्यमान × त्वरण होता है।

अर्थात्, F = m × a

उदाहरण 8.1

प्रश्न:
एक 5 kg द्रव्यमान वाली वस्तु पर 2 s के लिए एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3 m/s से बढ़ाकर 7 m/s कर देता है।
(क) लगाए गए बल की मात्रा ज्ञात करें।
(ख) यदि यही बल 5 s तक कार्य करे, तो वस्तु का अंतिम वेग क्या होगा?

हल:

हमें ज्ञात हैं:

परिमाण	प्रतीक	मान
द्रव्यमान	m	5 kg
प्रारंभिक वेग	u	3 m/s
अंतिम वेग	v	7 m/s
समय	t	2 s

(क) लगाए गए बल की गणना:

न्यूटन के द्वितीय नियम के अनुसार:

F = m × (v − u) / t

मान रखने पर:

F = 5 × (7 − 3) / 2
= 5 × 4 / 2
= 10 N

अतः लगाया गया बल = 10 न्यूटन।

(ख) जब यही बल 5 s तक लगाया जाए:

हम जानते हैं,

F = m × (v − u) / t या v = u + (F × t) / m

मान रखने पर:

v = 3 + (10 × 5) / 5
= 3 + 10
= 13 m/s

अंतिम उत्तर:

बल = 10 N
अंतिम वेग (5 s के बाद) = 13 m/s

उदाहरण 8.2

प्रश्न:
किसमें अधिक बल की आवश्यकता होगी:

2 kg द्रव्यमान वाली किसी वस्तु को 5 m/s² की दर से त्वरित करने में, या
4 kg द्रव्यमान वाली वस्तु को 2 m/s² की दर से त्वरित करने में?

हल:

न्यूटन के द्वितीय नियम के अनुसार:

F = m × a

चरण 1: पहले विकल्प के लिए बल:

द्रव्यमान = 2 kg, त्वरण = 5 m/s²

F₁ = m × a = 2 × 5 = 10 N

चरण 2: दूसरे विकल्प के लिए बल:

द्रव्यमान = 4 kg, त्वरण = 2 m/s²

F₂ = m × a = 4 × 2 = 8 N

निष्कर्ष:

F₁ = 10 N > F₂ = 8 N
अतः 2 kg द्रव्यमान वाली वस्तु को 5 m/s² की दर से त्वरित करने के लिए अधिक बल की आवश्यकता होगी।

उदाहरण 8.3

प्रश्न:
एक कार 108 km/h की गति से चल रही है और ब्रेक लगाने के बाद यह रुकने में 4 s का समय लेती है।
कार का यात्रियों सहित कुल द्रव्यमान = 1000 kg।
ब्रेक लगाने के बाद कार पर लगने वाले बल की गणना करें।

हल:

न्यूटन के द्वितीय नियम के अनुसार,

F = m × a

चरण 1: गति को SI इकाई में बदलें

गति v = 108 km/h = 108 × 1000 / 3600 m/s = 30 m/s

चूंकि कार रुक रही है, अंतिम वेग u = 0 m/s

चरण 2: त्वरण (a) ज्ञात करें

त्वरण = (अंतिम वेग − प्रारंभिक वेग) / समय

a = (0 − 30) / 4 = −7.5 m/s²

नकारात्मक चिह्न दर्शाता है कि त्वरण दिशा में बल गति के विपरीत है।

चरण 3: बल की गणना

द्रव्यमान m = 1000 kg

F = m × a = 1000 × (−7.5) = −7500 N

नकारात्मक चिह्न बताता है कि बल गति के विपरीत है।

अंतिम उत्तर:

लगने वाला बल = 7500 N (गति के विपरीत दिशा में)

उदाहरण 8.4

प्रश्न:
एक बल F = 45 N किसी द्रव्यमान m₁ को 10 m/s² का त्वरण देता है और द्रव्यमान m₂ को 20 m/s² का त्वरण देता है।
यदि दोनों द्रव्यमानों को एक साथ जोड़ा जाए, तो इसी बल के द्वारा उत्पन्न त्वरण ज्ञात कीजिए।

हल:

चरण 1: पहले द्रव्यमान m₁ ज्ञात करें

न्यूटन के द्वितीय नियम के अनुसार:

F = m₁ × a₁

45 = m₁ × 10

m₁ = 45 / 10 = 4.5 kg

चरण 2: दूसरे द्रव्यमान m₂ ज्ञात करें

F = m₂ × a₂

45 = m₂ × 20

m₂ = 45 / 20 = 2.25 kg

चरण 3: संयुक्त द्रव्यमान पर त्वरण ज्ञात करें

संयुक्त द्रव्यमान: m = m₁ + m₂ = 4.5 + 2.25 = 6.75 kg

उसी बल F = 45 N के द्वारा उत्पन्न त्वरण:

a = F / (m₁ + m₂)

a = 45 / 6.75 ≈ 6.67 m/s²

अंतिम उत्तर:

संयुक्त द्रव्यमान पर त्वरण ≈ 6.67 m/s²

उदाहरण 8.5

प्रश्न:
एक लंबी मेज पर सीधी रेखा में जा रही 20 g द्रव्यमान वाली गेंद का वेग-समय ग्राफ (चित्र 8.9) दिया गया है।
गेंद को विरामावस्था में लाने के लिए मेज द्वारा कितना बल लगेगा?

हल:

चरण 1: द्रव्यमान को SI इकाई में बदलें

m = 20 g = 0.020 kg

चरण 2: वेग-समय ग्राफ से त्वरण ज्ञात करें

यदि v प्रारंभिक वेग और t ब्रेक लगने का समय है, तो

a = (v_final − v_initial) / t

चूंकि अंतिम वेग v_final = 0 (गेंद रुक जाती है):

a = (0 − v_initial) / t = − v_initial / t

चरण 3: बल ज्ञात करें

न्यूटन के द्वितीय नियम के अनुसार:

F = m × a = 0.020 × (− v_initial / t) = −0.020 × (v_initial / t) N

नकारात्मक चिह्न दर्शाता है कि बल वेग की दिशा के विपरीत कार्य करता है।

अंतिम उत्तर:

मेज़ द्वारा लगाया गया बल = 0.020 × (v_initial / t) N (गति के विपरीत दिशा में)

नोट: v_initial और t ग्राफ से पढ़कर मान रखकर अंतिम न्यूटन में बल ज्ञात किया जा सकता है।

गति का तृतीय नियम (Newton’s Third Law of Motion)

न्यूटन का गति का तृतीय नियम कहता है:

“प्रत्येक क्रिया के लिए समान और विपरीत प्रतिक्रिया होती है।”
यानी जब कोई वस्तु किसी अन्य वस्तु पर बल लगाती है, तो दूसरी वस्तु भी उस वस्तु पर समान मात्रा में लेकिन विपरीत दिशा में बल लगाती है।

उदाहरण और व्याख्या:

जब आप जमीन पर कदम रखते हैं, तो आपका पैर जमीन पर बल लगाता है (क्रिया), और जमीन भी आपको पीछे की ओर समान बल लगाती है (प्रतिक्रिया), जिससे आप आगे बढ़ते हैं।
एक रॉकेट के उड़ने का सिद्धांत भी इसी नियम पर आधारित है। रॉकेट ईंधन जलता है और गैस को नीचे की ओर फेंकता है (क्रिया), और रॉकेट को ऊपर की ओर धकेलने वाला बल (प्रतिक्रिया) उत्पन्न होता है।
पानी में तैरते समय, जब आप हाथ से पानी को पीछे की ओर धकेलते हैं, तो पानी आपको आगे की ओर धकेलता है।

गणितीय रूप में:

यदि किसी वस्तु A द्वारा वस्तु B पर बल F_AB लगाया जाता है, तो वस्तु B द्वारा वस्तु A पर बल होगा:

F_BA = − F_AB

यहाँ नकारात्मक चिह्न बल की विपरीत दिशा को दर्शाता है।

महत्वपूर्ण बिंदु:

क्रिया और प्रतिक्रिया हमेशा अलग-अलग वस्तुओं पर लगते हैं।
वे कभी एक ही वस्तु पर नहीं लग सकते।
क्रिया और प्रतिक्रिया बल हमेशा एक-दूसरे के समान मान के होते हैं।
वे हमेशा विपरीत दिशा में कार्य करते हैं।

दैनिक जीवन में उदाहरण:

पक्षी अपने पंखों से हवा को नीचे धकेलता है और प्रतिक्रिया में ऊपर उड़ता है।
बोट के पैडल को पानी में पीछे की ओर धकेलने पर बोट आगे बढ़ती है।
गेंद को दीवार पर फेंकने पर दीवार गेंद को पीछे फेंकती है।

सारांश:

न्यूटन का तृतीय नियम कहता है कि “हर क्रिया के लिए समान और विपरीत प्रतिक्रिया होती है”।
यह नियम सभी प्रकार की गतियों और बलों के लिए मान्य है और हमारे रोजमर्रा के जीवन में भी दिखाई देता है।

अभ्यास

प्रश्न 1:

कोई वस्तु शून्य बाह्य असंतुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशून्य वेग से गति करना संभव है? यदि हाँ, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख करें। यदि नहीं, तो कारण स्पष्ट करें।

उत्तर:
हाँ, संभव है। यदि किसी वस्तु पर कोई असंतुलित बाह्य बल नहीं लगता है (बल शून्य है), तो वस्तु अपनी वर्तमान गति में (अशून्य या अशून्य वेग) समान वेग और दिशा में लगातार गति करती रहेगी।
शर्तें:

वस्तु पर कोई बाह्य असंतुलित बल नहीं लगना चाहिए।
वस्तु किसी रुकावट या घर्षण के प्रभाव में नहीं होनी चाहिए।

प्रश्न 2:

जब किसी छड़ी से एक दरी (कार्पेट) को पीटा जाता है, तो धूल के कण बाहर आ जाते हैं। स्पष्ट करें।

उत्तर:
छड़ी द्वारा दरी को पीटने पर दरी पर असंतुलित बल कार्य करता है। धूल के कणों का द्रव्यमान बहुत कम होता है और उनका जड़त्व भी कम होता है। इसलिए वे तुरंत दरी से अलग होकर हवा में उड़ जाते हैं। यह न्यूटन के गति के पहले और दूसरे नियम के अनुसार है।

प्रश्न 3:

बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है?

उत्तर:
जब बस चलती है या अचानक रुकती है, तो सामान अपनी जड़त्व के कारण अपनी स्थिति बनाए रखना चाहता है। यदि सामान को बाँधा न जाए, तो वह आगे या पीछे खिसक सकता है और दुर्घटना का कारण बन सकता है। रस्सी का उपयोग सामान को स्थिर रखने और सुरक्षा सुनिश्चित करने के लिए किया जाता है।

प्रश्न 4:

किसी बल्लेबाज द्वारा क्रिकेट की गेंद को मारने पर गेंद जमीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि:

(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है।
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।
(d) गेंद पर कोई असंतुलित बल कार्यरत नहीं है, अतः गेंद विरामावस्था में आने के लिए प्रयासरत है।

सही विकल्प: (c)
व्याख्या: गेंद को रुकने के लिए उसकी गति के विपरीत दिशा में बल कार्य करता है। यह बल मुख्य रूप से घर्षण बल है जो गेंद को धीरे-धीरे रोक देता है।

प्रश्न 5:

एक ट्रक विरामावस्था से किसी पहाड़ी से नीचे नियत त्वरण से लुढ़कना शुरू करता है। यह 20 s में 400 m की दूरी तय करता है। इसका त्वरण ज्ञात करें। यदि इसका द्रव्यमान 7 टन है, तो इस पर लगने वाले बल की गणना करें। (1 टन = 1000 kg)

हल:

दूरी s = 400 m, प्रारंभिक वेग u = 0, समय t = 20 s

समीकरण: s = ut + 1/2 a t²

400 = 0 + 1/2 × a × 20²

400 = 1/2 × a × 400

a = 2 m/s²

द्रव्यमान m = 7 टन = 7000 kg

F = m × a = 7000 × 2 = 14000 N

उत्तर: त्वरण = 2 m/s², बल = 14000 N

—

प्रश्न 6:

1 kg द्रव्यमान के एक पत्थर को 20 m/s की गति से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50 m की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ के बीच लगने वाले घर्षण बल की गणना करें।

हल:

दूरी s = 50 m, प्रारंभिक वेग u = 20 m/s, अंतिम वेग v = 0, द्रव्यमान m = 1 kg

समीकरण: v² = u² + 2 a s

0 = 20² + 2 × a × 50

0 = 400 + 100 a

a = −4 m/s²

F_friction = m × a = 1 × 4 = 4 N

उत्तर: घर्षण बल = 4 N (गति के विपरीत दिशा में)

—

प्रश्न 7:

एक 8000 kg द्रव्यमान का रेल इंजन 2000 kg द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। इंजन 40000 N का बल आरोपित करता है। पटरी 5000 N का घर्षण बल लगाती है। ज्ञात करें:

(a) नेट त्वरण बल
(b) रेल का त्वरण

हल:

कुल द्रव्यमान m_total = 8000 + (5 × 2000) = 18000 kg

घर्षण बल F_friction = 5000 N, लागू बल F = 40000 N

(a) नेट बल: F_net = F – F_friction = 40000 – 5000 = 35000 N

(b) रेल का त्वरण: a = F_net / m_total = 35000 / 18000 ≈ 1.944 m/s²

उत्तर: नेट बल = 35000 N, त्वरण ≈ 1.944 m/s²

—

प्रश्न 8:

एक गाड़ी का द्रव्यमान 1500 kg है। यदि गाड़ी को 1.7 m/s² के ऋणात्मक त्वरण (अवमंदन) के साथ विरामावस्था में लाना है, तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा?

हल:

m = 1500 kg, a = 1.7 m/s² (ऋणात्मक)

F = m × a = 1500 × 1.7 = 2550 N

उत्तर: सड़क पर गाड़ी पर लगने वाला बल = 2550 N (गति के विपरीत)

—

प्रश्न 9:

किसी द्रव्यमान की वस्तु जिसका वेग है, का संवेग क्या होगा?

(a) mv
(b) mv
(c) 2mv
(d) mv

सही विकल्प: (a) mv
व्याख्या: संवेग (momentum) वस्तु के द्रव्यमान और वेग का गुणनफल होता है। p = m × v

प्रश्न 16:

अख्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं। अचानक उड़ता हुआ कोई कीड़ा गाड़ी के सामने के शीशे से टकराया और वह शीशे से चिपक गया। अख्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है। अख्तर ने कहा कि चूँकि कार का वेग बहुत अधिक था अतः कार ने कीड़े पर बहुत अधिक बल लगाया। राहुल ने कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ।

उत्तर और प्रतिक्रिया:
न्यूटन के तृतीय नियम के अनुसार, किसी भी क्रिया के लिए प्रतिक्रिया हमेशा समान और विपरीत होती है।
यानी, कीड़े और कार दोनों पर समान बल लगाया गया।

किरण की बात: संवेग परिवर्तन (Δp = mΔv) की बात सही है। चूँकि कीड़े का द्रव्यमान बहुत कम है और वेग में बड़ा परिवर्तन हुआ, इसलिए संवेग परिवर्तन छोटा होगा।
अख्तर की बात: कार का द्रव्यमान बहुत अधिक है, इसलिए वेग परिवर्तन बहुत छोटा होगा। बल समान है, लेकिन संवेग परिवर्तन का मान अलग होगा।
राहुल की बात: बल समान है, यह सही है। लेकिन संवेग परिवर्तन दोनों के लिए बराबर नहीं होता, क्योंकि Δp = F × Δt, और Δt समान होने पर भी द्रव्यमान के अनुसार संवेग परिवर्तन अलग होगा।

निष्कर्ष: बल समान होता है, लेकिन संवेग परिवर्तन की मात्रा द्रव्यमान और वेग परिवर्तन के कारण अलग होती है।

—

प्रश्न 17:

एक 10 kg द्रव्यमान की घंटी 80 cm की ऊँचाई से फर्श पर गिरी। इस अवस्था में घंटी द्वारा फर्श पर स्थानांतरित संवेग के मान की गणना करें। (गुरुत्वाकर्षण त्वरण g = 10 m/s²)

हल:

द्रव्यमान: m = 10 kg

ऊँचाई: h = 80 cm = 0.8 m

गुरुत्वाकर्षण त्वरण: g = 10 m/s²

चरण 1: अंतिम वेग ज्ञात करें

समीकरण: v² = u² + 2 g h

v² = 0 + 2 × 10 × 0.8 = 16

v = √16 = 4 m/s

चरण 2: संवेग (momentum) ज्ञात करें

p = m × v = 10 × 4 = 40 kg·m/s

उत्तर: फर्श पर स्थानांतरित संवेग = 40 kg·m/s

बल एवं गति के नियम – MCQs

किस नियम के अनुसार कोई वस्तु अपनी गति में तब तक बनी रहती है जब तक उस पर कोई असंतुलित बल कार्य न करे?
- (a) गति का प्रथम नियम
- (b) गति का द्वितीय नियम
- (c) गति का तृतीय नियम
- (d) गुरुत्वाकर्षण का नियम
न्यूटन का द्वितीय नियम किस समीकरण से व्यक्त किया जाता है?
- (a) F = ma
- (b) p = mv
- (c) F = m/v
- (d) a = F/m²
किसी वस्तु पर जितना अधिक बल लगाया जाएगा, उसका त्वरण:
- (a) कम होगा
- (b) अधिक होगा
- (c) बल पर निर्भर नहीं करेगा
- (d) द्रव्यमान पर निर्भर नहीं करेगा
न्यूटन के तृतीय नियम के अनुसार:
- (a) हर क्रिया के लिए समान और विपरीत प्रतिक्रिया होती है
- (b) कोई क्रिया नहीं होती
- (c) बल हमेशा अनुपस्थित रहता है
- (d) संवेग हमेशा शून्य होता है
यदि किसी वस्तु का द्रव्यमान बढ़ जाए और उसी बल को लगाया जाए, तो त्वरण:
- (a) बढ़ेगा
- (b) घटेगा
- (c) अपरिवर्तित रहेगा
- (d) अनिश्चित होगा
किसी वाहन पर अचानक ब्रेक लगाने पर यात्री आगे की ओर झुकते हैं। इसका कारण है:
- (a) जड़त्व
- (b) गुरुत्वाकर्षण
- (c) घर्षण
- (d) संवेग
संवेग (momentum) की परिभाषा है:
- (a) p = F × t
- (b) p = m × v
- (c) p = m × a
- (d) p = F/a
किस उदाहरण में जड़त्व अधिक होगा?
- (a) एक रबर की गेंद और उसी आकार का पत्थर
- (b) 1 kg और 2 kg का समान आकार का ईंट
- (c) दोनों बराबर
- (d) निर्भर नहीं करता
यदि कोई वस्तु गति में है और उस पर कोई असंतुलित बल नहीं लगता, तो वह:
- (a) रुक जाएगी
- (b) स्थिर रहेगी
- (c) समान वेग और दिशा में गति करती रहेगी
- (d) अनिश्चित गति करेगी
एक पत्थर पानी में गिरता है। पत्थर पर कौन-सा बल कार्य करता है जो उसकी गति को रोकता है?
- (a) गुरुत्वाकर्षण
- (b) घर्षण और प्रतिरोधी बल
- (c) जड़त्व
- (d) संवेग
यदि F = ma है और m = 10 kg, a = 2 m/s², तो F कितना होगा?
- (a) 5 N
- (b) 20 N
- (c) 10 N
- (d) 15 N
किसी वस्तु पर लगे बल का दिशा क्या होती है?
- (a) वस्तु की गति के समान
- (b) वस्तु की गति के विपरीत
- (c) हमेशा नीचे की ओर
- (d) बल की दिशा में
किसी वाहन की अचानक गति बढ़ने पर यात्री पीछे की ओर झुकते हैं। यह उदाहरण दर्शाता है:
- (a) न्यूटन का प्रथम नियम
- (b) न्यूटन का द्वितीय नियम
- (c) न्यूटन का तृतीय नियम
- (d) गुरुत्वाकर्षण
किसी वस्तु के संवेग में परिवर्तन किस पर निर्भर करता है?
- (a) बल और समय
- (b) द्रव्यमान और वेग
- (c) केवल बल
- (d) केवल द्रव्यमान
यदि कोई वाहन रुकता है, तो उसका संवेग:
- (a) बढ़ता है
- (b) घटता है
- (c) स्थिर रहता है
- (d) अनिश्चित है
न्यूटन का तृतीय नियम किस प्रकार की क्रिया पर लागू होता है?
- (a) बल की क्रिया और प्रतिक्रिया
- (b) केवल संवेग परिवर्तन
- (c) केवल गति परिवर्तन
- (d) कोई भी नहीं
जड़त्व का परिमाण किससे प्रभावित होता है?
- (a) द्रव्यमान
- (b) गति
- (c) बल
- (d) समय
एक वाहन की गति में वृद्धि करने के लिए क्या करना होगा?
- (a) बल लगाया जाए
- (b) बल हटाया जाए
- (c) जड़त्व बढ़ाई जाए
- (d) संवेग घटाया जाए
किसे असंतुलित बल कहा जाता है?
- (a) एक ही दिशा में कार्यरत सभी बल
- (b) बराबर और विपरीत दिशा के बल
- (c) कोई बल नहीं
- (d) बराबर बल
एक वस्तु का संवेग यदि m = 2 kg और v = 5 m/s हो, तो p = ?
- (a) 10 kg·m/s
- (b) 7 kg·m/s
- (c) 5 kg·m/s
- (d) 12 kg·m/s

बल एवं गति के नियम – MCQ उत्तर

प्रश्न संख्या	सही उत्तर
1	a) गति का प्रथम नियम
2	a) F = ma
3	b) अधिक होगा
4	a) हर क्रिया के लिए समान और विपरीत प्रतिक्रिया होती है
5	b) घटेगा
6	a) जड़त्व
7	b) p = m × v
8	b) 2 kg का ईंट
9	c) समान वेग और दिशा में गति करती रहेगी
10	b) घर्षण और प्रतिरोधी बल
11	b) 20 N
12	d) बल की दिशा में
13	a) न्यूटन का प्रथम नियम
14	a) बल और समय
15	b) घटता है
16	a) बल की क्रिया और प्रतिक्रिया
17	a) द्रव्यमान
18	a) बल लगाया जाए
19	a) एक ही दिशा में कार्यरत सभी बल
20	a) 10 kg·m/s

बल एवं गति के नियम के बारे और अधिक जानने के लिए –

Rea more chapters